- КАНТОРА ТЕОРЕМА
- 1) Множество 2A, состоящее из всех подмножеств множества А, не равномощно ни самому А, ни его подмножеству. Идея доказательства этой теоремы, принадлежащая Г. Кантору (G.Cantor, 1878), получила название "канторова диагонального метода" и играет существенную роль в теории множеств. Из К. т. следует, что никакие два из множеств А,
 не равномощны. Таким способом получается бесконечно много различных кардинальных чисел. Из К. т. вытекает, что не существует множества всех множеств. Это означает, что нельзя принять аксиому теории множеств, утверждающую существование для каждой высказывательной функции Ф (х)множества, состоящего из элементов х, удовлетворяющих Ф(х)(СМ. [1], [2], [3], [8]).
не равномощны. Таким способом получается бесконечно много различных кардинальных чисел. Из К. т. вытекает, что не существует множества всех множеств. Это означает, что нельзя принять аксиому теории множеств, утверждающую существование для каждой высказывательной функции Ф (х)множества, состоящего из элементов х, удовлетворяющих Ф(х)(СМ. [1], [2], [3], [8]).Б. А. Ефимов.
2) Любая последовательность убывающих ограниченных замкнутых множеств действительных чисел имеет непустое пересечение. Обобщается на компактные подмножества метрич. пространства. Свойство: диаметры замкнутых множеств метрич. пространства X, последовательно вложенных друг в друга, стремятся к нулю - одно из определений полноты X. Свойство: вполне упорядоченная система убывающих замкнутых множеств топологич. пространства X- одно из определений бикомпактности X(см. [1], [2], [4], [5], [11]).
3) Всякое множество действительных чисел есть объединение совершенного множества своих конденсации точек и счетного множества; иногда наз. теоремой Кантора - Бендиксона. Обобщена на случай подмножеств метрич. пространства со счетной
базой (теорема Линделёфа) (см. [1], [2], [3], [14], [15]).
4) Если из двух множеств каждое эквивалентно части другого, то эти два множества эквивалентны между собою. Аналогичное утверждение справедливо и для вполне упорядоченных множеств. Иногда наз. теоремой Кантора - Бернштейна или просто теоремой Бернштейна (последний дал корректное доказательство этой теоремы) (см. [1], [2], [3], [10], [12], [16]).
5) Если
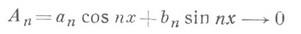 для всех, кроме конечного числа, точек отрезка [-p, p], то а п,
для всех, кроме конечного числа, точек отрезка [-p, p], то а п, Обобщена на случаи, когдана
Обобщена на случаи, когдана 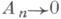 множестве положительной меры (теорема Лебега), когда
множестве положительной меры (теорема Лебега), когда  на множестве второй категории (теорема Юнга), и на другие ситуации. Важнейшим следствием являются различные теоремы о множествах единственности тригонометрпч. рядов (см. [1], [6], [7], [9], [18], [19]).
на множестве второй категории (теорема Юнга), и на другие ситуации. Важнейшим следствием являются различные теоремы о множествах единственности тригонометрпч. рядов (см. [1], [6], [7], [9], [18], [19]).6) Функция, непрерывная на замкнутом отрезке действительной оси, равномерно непрерывна на нем. Обобщена на случай непрерывных отображений бикомпактного пространства в равномерное пространство. Иногда наз. теоремой Гейне - Кантора (см. [1], [4], [5], [13]).
Лит.:[1] Cantor G., Gesammelte Abhandlungen, В., 1932; [2] Хаусдорф Ф., Теория множеств, пер. с нем., М.- Л., 1937; [3] Куратовский К., Мостовский А., Теория множеств, пер. с англ., М., 1970; [4] Александров П. С, Введение в теорйю множеств и общую топологию, М., 1977; [э] Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968; [6] Бари Н. К., Тригонометрические ряды, М., 1961; .[7] Уиттекер Э. Т., Ваг сон Дж. Н., Курс современного анализа, 2 изд., т. 1, пер. с англ., М., 1963; [8] Сantor G., "J. reine und angew. Math.", 1878, Bd 84, S. 242-58; [9] eго же, "Math. Ann.", 1871, Bd 4, S. 139-43; [10] его же, там же, 1897, Bd 49, S. 207-46; [11] его же, там же, 1880, Bd 17, S. 355-58; [12] Bore 1 Е., Lecons sur la theorie des fonctions, P., 1898; [13] Heine E., "J. reine und angew. Math.", 1872, Bd 74, S. 172; [14] Lin del of E., "Acta math.", 1905, v.29, p. 183-90; [15] Cantor G., "J. reine und angew. Math.", 1870, Bd 72, S. 130-42: [16] его же, "Math. Ann.", 1883, Bd 21, S. 51-58; [17] Bendixson I., "Acta math.", 1883, v. 2, p. 415-29; [18] Lebesgue H., Lecons sur les series trigonometriques..., P., 1906; [19] Young W. H., "Proc. Roy. Soc", 1912, v. 87, p. 331-39; [20] Бурбаки Н., Очерки по истории математики, пер. с франц., М., 1963.
М. И. Войцеховский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
