ПОЛУГРУППА С УСЛОВИЕМ КОНЕЧНОСТИ

- полугруппа, обладающая нек-рым свойством q таким, что всякая конечная полугруппа обладает этим свойством (такое свойство q наз. условием конечности). В определении свойства q могут фигурировать элементы полугруппы, ее подполугруппы и т. п.

Примеры условий конечности: периодичность (см. Периодическая полугруппа), локальная конечность (см. Локально конечная полугруппа), финитная аппроксимируемость (см. Финитно аппроксимируемая полугруппа), конечная порожденность, конечная определенность. Исследования конечно определенных полугрупп в значительной степени ведутся с точки зрения алгоритмич. проблем. Наиболее известное условие, при к-ром конечная порожденность полугруппы влечет ее конечную определенность,- коммутативность (теорема Редеи). Всякая счетная полугруппа вложима в полугруппу с двумя порождающими, а также в полугруппу-с тремя идемпотентными порождающими [8].

Целый ряд условий конечности формулируется в терминах решетки подполугрупп (напр., условие минимальности для подполугрупп). Полугруппа Sтогда и только тогда удовлетворяет условию минимальности для подполугрупп, когда Sпериодическая, имеет лишь конечное число классов кручения, в каждом классе кручения К _е наибольшая подгруппа G_e удовлетворяет условию минимальности для подгрупп, а разность 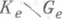конечна [2]. Аналогичное строение имеют полугруппы конечного ранга (конечность ранга означает, что минимальное число порождающих каждой конечно порожденной подполугруппы полугруппы Sне превосходит фиксированного числа), полугруппы конечной ширины (конечность ширины для Sозначает, что из любого конечного множества Мее элементов можно выделить подмножество, порождающее ту же подполугруппу, что и М, мощность к-рого не превосходит фиксированного числа), периодические полугруппы с условием максимальности для подполугрупп и др. (см. [3], [4]).

Инверсная полугруппа удовлетворяет условию минимальности для инверсных подполугрупп тогда и только тогда, когда она обладает главным рядом (см. Идеальный ряд полугруппы), каждый фактор к-рого есть Брандта полугруппа с конечным числом идемпотентов, все максимальные подгруппы к-рой удовлетворяют условию минимальности для подгруппы. Аналогичные описания получены для условия максимальности, конечности ранга и др. (см. [5]).

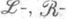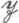Из условий конечности, формулируемых в терминах частично упорядоченного множества идеалов полугруппы, наиболее известны условия минимальности M_L, M_R, M_J для главных левых, правых, двусторонних идеалов (эти условия часто определяются в терминах и -классов, см. Грина отношения эквивалентности). Аналогично определяется условие М _H для 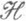классов. Конъюнкция условий M_L и M_R эквивалентна Конъюнкции условий M_J и М _H, в остальном эти условия независимы; в частности, полугруппа с условиями M_L и M_J не обязательно удовлетворяет условиям M_R и M_H. Вместе с тем полупростая (см. Главный фактор полугруппы) полугруппа с условием M_L или M_R удовлетворяет условию M_J. Для регулярных полугрупп все четыре условия эквивалентны; всякая полугруппа с условием М _H будет квазипериодической. Конечно порожденная полугруппа с условием M_L или M_R, все подгруппы к-рой конечны, сама конечна [6].

Полугруппа с условием минимальности для правых конгруэнции является периодической, удовлетворяет условию M_L и двойственному условию максимальности для главных левых идеалов; если при этом все ее подгруппы конечны, то сама полугруппа конечна [6]. В инверсных полугруппах условие минимальности для правых конгруэнции эквивалентно условию минимальности для левых конгруэнции, а также тому, что полугруппа имеет лишь конечное число идемпотентов и удовлетворяет условию минимальности для подгрупп [7]. Изучен ряд свойств полугрупп с условием максимальности для односторонних конгруэнции. Коммутативная полугруппа удовлетворяет условию минимальности (максимальности) для конгруэнции тогда и только тогда, когда она имеет главный ряд и удовлетворяет условию минимальности для подгрупп [7] (конечно порождена).

Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 2, М., 1972; [2] Шеврин Л. Н., "Изв. АН СССР. Сер. матем.", 1965, т. 29, № 3, с. 553-С6; [3] его же,"Матем. заметки", 1974, т. 15, № 6, с. 925-35; [4] его же, "Изв. ВУЗов. Матем.", 1974, №5, с. 205-15; [5] Ершова Т. И., там же, 1977, № 11, с. 7 - 14; [6] Hotzel Е., "J. Algebra", 1979, v. 60, №2, p. 352 - 70; [7] Kozhulchov I. В., "Semigroup Forum", 1980, v. 21, № 4, p. 337-50; [8] Pastijn F., там же, 1977, v. 14, № 3, p. 247-64. Л. H. Шеврин.