- ОТДЕЛИМОСТИ АКСИОМА
- условие, налагаемое на топологич. пространство и выражающее требование, чтобы те или иные дизъюнктные, т. е. не имеющие общих точек, множества были в нек-ром определенном смысле топологически отделены друг от друга. Простейшие, т. е. самые слабые из этих аксиом, касаются лишь одноточечных множеств, т. е. точек пространства. Это т. п. аксиомы Т 0 (аксиома Колмогорова) п T1. Дальнейшие суть Т 2 (аксиома Xаусдорфа), Т 3 (аксиома регулярности) и T4 (аксиома нормальности), требующие, соответственно, чтобы всякие две различные точки (аксиома Т 2), всякая точка и всякое не содержащее ее замкнутое множество(аксиома Т 3), всякие два дизъюнктные замкнутые множества (аксиома T4).были отделимы окрестностями, т. е. содержались в дизъюнктных открытых множествах данного пространства.
Топологич. Пространство, удовлетворяющее аксиоме
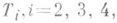 наз. Т i- пространством, Т 2 -пространство наз. хаусдорфовым, а T3 -пространство - регулярным; хаусдорфово T4 -пространство всегда регулярно и наз. нормальным.
наз. Т i- пространством, Т 2 -пространство наз. хаусдорфовым, а T3 -пространство - регулярным; хаусдорфово T4 -пространство всегда регулярно и наз. нормальным.
Особое место занимает т. н. функциональная отделимость. Два множества Аи Вв данном топологич. пространстве Xназ. функционально отделимыми в X, если существует такая определенная во всем пространстве действительная ограниченная непрерывная функция f, к-рая принимает во всех точках множества Аодно значение а, а во всех точках множества В - нек-рое отличное от азначение b. При этом всегда можно предположить, что
 во всех точках
во всех точках 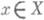
Два функционально отделимых множества всегда отделимы и окрестностями, обратное утверждение верно не всегда. Однако имеет место лемма Урысона: в нормальном пространстве всякие два дизъюнктные замкнутые множества функционально отделимы. Пространство, в к-ром всякая точка функционально отделима от всякого не содержащего ее замкнутого множества, наз. вполне регулярным. Вполне регулярное T2 -пространство наз. тихоновским.
Лит.:[1] Александров П. С., Введение в теорию множеств и общую топологию, М., 1977. В. И. Зайцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
