НОРМАЛЬНОЕ ПРОСТРАНСТВО

НОРМАЛЬНОЕ ПРОСТРАНСТВО

- топологическое пространство, удовлетворяющее аксиоме 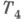(см. Отделимости аксиома), т. е. такое топологич. пространство, в к-ром одноточечные множества замкнуты и любые два дизъюнктные замкнутые множества отделимы окрестностями (т. е. содержатся в дизъюнктных открытых множествах). Н. п. образуют частный случай вполне регулярных пространств (тихоновских), особенно важный для размерности теории. Всякое замкнутое подпространство Н. п. нормально (нормальность наследуется по замкнутым множествам). Пространства, все подпространства к-рых нормальны, наз. наследственно нормальными. Для наследственной нормальности достаточно, чтобы все его открытые подпространства были Н. п. Для наследственной нормальности пространства необходимо и достаточно, чтобы были отделимы окрестностями всякие два множества, из к-рых ни одно не содержит точек соприкосновения другого. Н. п. наз. совершенно нормальным, если в нем каждое замкнутое множество является пересечением счетного числа открытых множеств. Всякое совершенно Н. п. есть наследственно Н. п.

Произведение двух Н. п. не обязано быть Н. п., и даже произведение Н. п. на отрезок может быть не нормальным.

Существуют важные классы пространств, более общие, чем нормальные, и менее общие, чем вполне регулярные. Среди этих пространств, близких к нормальным, первыми [2] были т. н. кваз и нормальные, или я-нормальпые, пространства. Это - тихоновские пространства, в к-рых отделимы окрестностями всякие два дизъюнктные p-множества, т. е. множества, являющиеся пересечением копечного числа замкнутых канонических множеств. Тихоновские пространства, в к-рых отделимы окрестностями всякие два дизъюнктные замкнутые канонич. множества, наз. -нормальным и [3];c-нормальные пространства, в к-рых каждое замкнутое канонич. множество является пересечением счетного числа открытых канонич. множеств, наз. совершенно c-н ормальными. Классы тихоновских c-нормальных, квазинормальных и, наконец, совершенно c-нормальных пространств идут последовательно убывая, причем никакие два из этих классов не совпадают между собою.

Лит.:[1] Александров П. С, Введение в теорию множеств и общую топологию, М., 1977; [2] 3айцев В. И., "Вестн. Моск. ун-та. Матем., механ.", 1967, № 3, с. 48-57; [3] Щепин Е. В., "Сиб. матем. ж.", 1972, т. 13, №5, с. 1182-1196.

П. С. Александров.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "НОРМАЛЬНОЕ ПРОСТРАНСТВО" в других словарях:

  • Нормальное пространство — Нормальное пространство  топологическое пространство, удовлетворяющее аксиомам отделимости T1, T4, то есть такое топологическое пространство, в котором одноточечные множества замкнуты и любые два непересекающихся замкнутых множества отделимы …   Википедия

  • НОРМАЛЬНОЕ ПРОСТРАНСТВО — в нек рой точке Рк поверхности пространства ортогональное дополнение к касательному пространству (см. Аналитическое пространство )в точке Рповерхности F. Размерность Н. п. равна п т(коразмерность поверхности F). Любое его одномерное… …   Математическая энциклопедия

  • СОВЕРШЕННО НОРМАЛЬНОЕ ПРОСТРАНСТВО — нормальное пространство, каждое замкнутое подмножество к рого имеет тип …   Математическая энциклопедия

  • ПРОСТРАНСТВО ЖИЗНЕННОЕ — 1) средняя площадь, приходящаяся на одну особь данной популяции и обеспечивающая нормальное существование особи в составе популяции; 2) территория, необходимая для удовлетворения всех нужд одного человека. Экологический энциклопедический словарь …   Экологический словарь

  • ВПОЛНЕ НОРМАЛЬНОЕ ПРОСТРАНСТВО — пространству, в к ром для любых двух подмножеств А, В, удовлетворяющих условиям имеются дизъюнктные окрестности; здесь замыкания множеств Аи В, a пустое множество. В. н. п. и только они наследственно нормальны. Совершенно нормальные пространства… …   Математическая энциклопедия

  • БЕСКОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО — нормальное T1 пространство X(см. Нормальное пространство).такое, что ни для какого не выполняется неравенство и для любого найдется такое конечное открытое покрытие пространства , что любое вписанное в конечное открытое покрытие этого… …   Математическая энциклопедия

  • НОРМАЛЬНОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО — аналитическое пространство, локальные кольца всех точек к рого нормальны, т. е. являются цело вамкнутыми областями целостности. Точка ханалитич. пространства Xназ. нормальной (говорят также, что Xнормально в точке х), если локальное кольцо… …   Математическая энциклопедия

  • МЕТРИЗУЕМОЕ ПРОСТРАНСТВО — пространство, топология к рого порождается иек рой метрикой по правилу: точка принадлежит замыканию множества в том и только в том случае, если она лежит на нулевом расстоянии от этого множества. Если такая метрика существует, то она не… …   Математическая энциклопедия

  • СЧЕТНОМЕРНОЕ ПРОСТРАНСТВО — нормальное пространство X, представимое в виде суммы своих подпространств X;размерности dim М. И. Войцеховский …   Математическая энциклопедия

  • Нормальное развитие (normal development) — Под развитием понимается функциональная адаптация индивидуума, происходящая в результате взаимодействия нормального физиолог. роста со средовым опытом, опосредствованным развивающимся индивидуумом. Последовательность стадий развития не является… …   Психологическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»