- ОТДЕЛИМОСТЬ МНОЖЕСТВ
- одно из основных понятий дескриптивной теории множеств (введенное Н. Н. Лузиным [1]). Служит важным инструментом для исследования дескриптивной природы множеств. Говорят, что множества Аи А' отделимы при помощи множеств, обладающих свойствами Р, если существуют обладающие свойством Рмножества Ви В' такие, что

Основополагающие результаты по отделимости принадлежат Н. Н. Лузину и П. С. Новикову. В дальнейшем не только появились многочисленные варианты теорем отделимости, но и само понятие О. м. было обобщено и получило новые формы. Одно из таких обобщений связано со следующей теоремой Новикова [2]: пусть {А п} - последовательность А-множеств полного сепарабельного метрич. пространства такая, что
 , тогда существует последовательность {В п} борелевских множеств такая, что
, тогда существует последовательность {В п} борелевских множеств такая, что  ,
,  , и
, и  . Эта теорема и различные ее варианты и обобщения получили название теорем кратной (или обобщенной) отделимос т и.
. Эта теорема и различные ее варианты и обобщения получили название теорем кратной (или обобщенной) отделимос т и.
Классич. результаты относятся к множествам, лежащим в полных сепарабельных метрич. пространствах. В хаусдорфовом пространстве X:1) два непересекающихся аналитич. множества отделимы борелевскими множествами, порожденными системой G открытых множеств этого пространства [3] (если X - Урысона пространство, то "G открытых" можно заменить на "F замкнутых"; в хаусдорфовом пространстве этого сделать, вообще говоря, нельзя [4]); 2) пусть
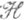 - нек-рая система A-множеств, порожденных системой F;если Аесть A-множество, порожденное системой
- нек-рая система A-множеств, порожденных системой F;если Аесть A-множество, порожденное системой  , и В - аналитич. множество,
, и В - аналитич. множество,  , то существует борелевское множество С, порожденное системой
, то существует борелевское множество С, порожденное системой  , такое, что
, такое, что  (см. [5]).
(см. [5]).
В отличие от этих (и других) вариантов первого принципа отделимости многие формулировки второго принципа отделимости не зависят от топологии пространства, в к-ром лежат рассматриваемые множества. Одна из них [6]: пусть система
 подмножеств данного множества замкнута относительно операции перехода к дополнению и содержит
подмножеств данного множества замкнута относительно операции перехода к дополнению и содержит  ; пусть {А п} - произвольная последовательность СА-множеств, порожденных системой
; пусть {А п} - произвольная последовательность СА-множеств, порожденных системой  ; тогда существует последовательность {С n} попарно непересекающихся СA-множеств, порожденных системой
; тогда существует последовательность {С n} попарно непересекающихся СA-множеств, порожденных системой  ,такая, что
,такая, что 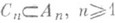 , и
, и  =
= (более точно, это - одна из формулировок принципа редукции, см. [7]).
(более точно, это - одна из формулировок принципа редукции, см. [7]).
Лит.:[1] Лузин Н. Н., Собр. соч., т. 2, М., 1958; [2] Новиков П. С., "Докл. АН СССР", 1934, т. 3 [т. 4], № 3, с. 145 - 148; [3] F rolik Z., "Czechosl. Math. J.", 1970, v. 20, p. 406-67; [4] Ostaszewski A. I., "Proc. London Math. Soc", 1973 v. 27, № 4, p. 649-66; [5] Rogers C. A., "J. London Math. Soc.", 1971, v. 3, № 1, p. 103-08; [6] eго жe, там же, 1973, v. 6, № 3, p. 491-5.03; [7] Куратовский К., Топология, [пер. с англ.], т. 1, М., 1966. А. Г. Елъкин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
