ОТДЕЛИМОЕ ПОПОЛНЕНИЕ КОЛЬЦА

ОТДЕЛИМОЕ ПОПОЛНЕНИЕ КОЛЬЦА

пополнение топологич. кольца , где А- топологич. кольцо, а 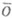- замыкание в Анулевого идеала о. О. п. к. снова является топологич. кольцом и обозначается обычно . Всякий непрерывный гомоморфизм кольца Ав полное отделимое кольцо В единственным образом продолжается до непрерывного гомоморфизма


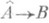
В наиболее важном случае, когда топология кольца Алинейна и задается фундаментальной системой идеалов 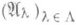, отделимое пополнение канонически отождествляется с проективным пределом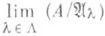


дискретных колец . Аналогично устроено отделимое пополнение модулей. В. И. Данилов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем сделать НИР

Смотреть что такое "ОТДЕЛИМОЕ ПОПОЛНЕНИЕ КОЛЬЦА" в других словарях:

  • АДИЧЕСКАЯ ТОПОЛОГИЯ — линейная топология кольца А, в к рой фундаментальная система окрестностей нуля образована степенями нек рого двустороннего идеала В этом случае топология наз. адической, а идеал идеалом определения топологии. Замыкание любого множества в… …   Математическая энциклопедия

  • ТОПОЛОГИЧЕСКОЕ КОЛЬЦО — кольцо R, являющееся топологич. пространством, причем требуется, чтобы отображения были непрерывны. Т. к. Rназ. отделимым, если оно отделимо как топологич. пространство. В этом случае пространство R хаусдорфово. Любое подкольцо МТ. к. R, а также… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»