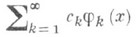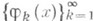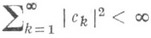ОРТОНОРМИРОВАННАЯ СИСТЕМА
- ОРТОНОРМИРОВАННАЯ СИСТЕМА
- 1) О. с. векторов - множество 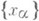 ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением (. , .) такое, что
ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением (. , .) такое, что 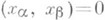 при
при 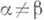 (ортогональность) и
(ортогональность) и 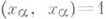 (нормируемость).
(нормируемость).
М. И. Войцеховский.
2) О. с. ф у н к ц и и - система 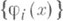 функций пространства L2(X, S,m,), являющаяся одновременно ортогональной и нормированной в L2(X, S,m), то есть
функций пространства L2(X, S,m,), являющаяся одновременно ортогональной и нормированной в L2(X, S,m), то есть
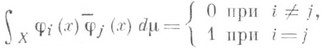
(см. Нормированная система, Ортогональная система). В математич. литературе часто термин "ортогональная система" означает "ортонормированная система". При исследовании данной ортогональной системы ее нормированность не играет существенной роли. Тем не менее нормированность систем дает возможность более ясной формулировки нек-рых теорем о сходимости рядов
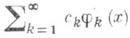
в терминах поведения коэффициентов 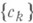 . Такой теоремой является, напр., теорема Рисса - Фигаера: ряд
. Такой теоремой является, напр., теорема Рисса - Фигаера: ряд
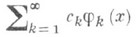
по ортонормированной в L2[a, b]системе 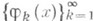
сходится в метрике пространства L2[a, b]тогда и только тогда, когда
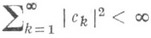
Лит.:[1] Колмогоров .А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [2] Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958. А. А. Талалян.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ОРТОНОРМИРОВАННАЯ СИСТЕМА" в других словарях:
Ортонормированная система — Ортонормированная система ортогональная система, у которой каждый элемент системы имеет единичную норму. Определение Для любых элементов этой системы скалярное произведение , где символ Кронекера. Ортонормированная система в случае… … Википедия
ОРТОНОРМИРОВАННАЯ СИСТЕМА ВЕКТОРОВ — множество ненулевых векторов векторного пространства X со скалярным произведением , где символы Кронекера = 0 при и = 1 при … Физическая энциклопедия
Ортонормированная система функций — Ортонормированная система элементов линейного пространства со скалярным произведением частный случай ортогональной системы, когда каждый элемент системы имеет единичную длину (в смысле расстояния, индуцируемого скалярным произведением). Для любых … Википедия
ПОЛНАЯ СИСТЕМА ФУНКЦИЙ — ортонормированная система функций {j(х)}нек рого гильбертова пространства Нтакая, что в H не существует функции, ортогональной всем функциям данного семейства. Система функций, полная в одном пространстве, может оказаться неполной в другом. Напр … Математическая энциклопедия
ЛАКУНАРНАЯ СИСТЕМА — порядка р>2, Sp система, ортонормированная система функций пространства Lp такая, что если ряд сходится в пространстве L2, то его сумма принадлежит классу Lp. Если система функций есть S р система при любом р>2, то она наз. системой. С.… … Математическая энциклопедия
ОРТОГОНАЛЬНАЯ СИСТЕМА — 1) О … Математическая энциклопедия
РАДЕМАХЕРА СИСТЕМА — ортонормированная на отрезке [0,1] система . Введена X. Радемахером [1]. Функции можно определить равенствами , ... Другое определение функций Радемахера получается путем рассмотрения двоичных разложений чисел отрезка [0,1]: если в двоичном… … Математическая энциклопедия
ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ — ортонормированная прямолинейная система координат в евклидовом пространстве. Д. п. с. к. на плоскости задается двумя взаимно перпендикулярными прямыми осями координат, на каждой из к рых выбрано положительное направление и задан отрезок единичной … Математическая энциклопедия
ЗАМКНУТАЯ СИСТЕМА — элементов, замкнутая система функций, система элементов jn некоторого линейного нормированного пространства Нтакая, что любой элемент можно сколь угодно точно приблизить в метрике пространства Нконечной линейной комбинацией элементов из этой… … Математическая энциклопедия
ОРТОГОНАЛЬНЫЙ БАЗИС — система попарно ортогональных элементов е 1, е 2, ..., е п, ... гильбертова пространства Xтакая, что любой элемент однозначно представим в виде сходящегося по норме ряда наз. рядом Фурье элемента хпо системе {е i}. Обычно базис { е i} выбирается… … Математическая энциклопедия
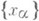 ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением (. , .) такое, что
ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением (. , .) такое, что 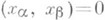 при
при 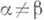 (ортогональность) и
(ортогональность) и 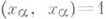 (нормируемость).
(нормируемость).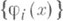 функций пространства L2(X, S,m,), являющаяся одновременно ортогональной и нормированной в L2(X, S,m), то есть
функций пространства L2(X, S,m,), являющаяся одновременно ортогональной и нормированной в L2(X, S,m), то есть 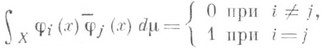
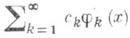
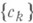 . Такой теоремой является, напр., теорема Рисса - Фигаера: ряд
. Такой теоремой является, напр., теорема Рисса - Фигаера: ряд