Ортонормированная система функций
- Ортонормированная система функций
-
Ортонорми́рованная система элементов линейного пространства со скалярным произведением — частный случай ортогональной системы, когда каждый элемент системы имеет единичную длину (в смысле расстояния, индуцируемого скалярным произведением).
Для любых элементов этой системы  скалярное произведение
скалярное произведение  , где δij — символ Кронекера.
, где δij — символ Кронекера.
Ортонормированная система в случае её полноты может быть использована в качестве базиса пространства. При этом разложение любого элемента 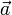 может быть вычислено по формулам:
может быть вычислено по формулам:  , где
, где  .
.
Примеры
- Функции
 образуют ортонормированную систему функций на конечном интервале [a,b] , если для них выполняется условие
образуют ортонормированную систему функций на конечном интервале [a,b] , если для них выполняется условие
 .
.
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Ортонормированная система функций" в других словарях:
ПОЛНАЯ СИСТЕМА ФУНКЦИЙ — ортонормированная система функций {j(х)}нек рого гильбертова пространства Нтакая, что в H не существует функции, ортогональной всем функциям данного семейства. Система функций, полная в одном пространстве, может оказаться неполной в другом. Напр … Математическая энциклопедия
ОРТОНОРМИРОВАННАЯ СИСТЕМА ВЕКТОРОВ — множество ненулевых векторов векторного пространства X со скалярным произведением , где символы Кронекера = 0 при и = 1 при … Физическая энциклопедия
ОРТОНОРМИРОВАННАЯ СИСТЕМА — 1) О. с. векторов множество ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением (. , .) такое, что при (ортогональность) и (нормируемость). М. И. Войцеховский. 2) О. с. ф у н к ц и и система функций пространства… … Математическая энциклопедия
Ортонормированная система — Ортонормированная система ортогональная система, у которой каждый элемент системы имеет единичную норму. Определение Для любых элементов этой системы скалярное произведение , где символ Кронекера. Ортонормированная система в случае… … Википедия
ЛАКУНАРНАЯ СИСТЕМА — порядка р>2, Sp система, ортонормированная система функций пространства Lp такая, что если ряд сходится в пространстве L2, то его сумма принадлежит классу Lp. Если система функций есть S р система при любом р>2, то она наз. системой. С.… … Математическая энциклопедия
ОРТОГОНАЛЬНАЯ СИСТЕМА — 1) О … Математическая энциклопедия
ЗАМКНУТАЯ СИСТЕМА — элементов, замкнутая система функций, система элементов jn некоторого линейного нормированного пространства Нтакая, что любой элемент можно сколь угодно точно приблизить в метрике пространства Нконечной линейной комбинацией элементов из этой… … Математическая энциклопедия
РАДЕМАХЕРА СИСТЕМА — ортонормированная на отрезке [0,1] система . Введена X. Радемахером [1]. Функции можно определить равенствами , ... Другое определение функций Радемахера получается путем рассмотрения двоичных разложений чисел отрезка [0,1]: если в двоичном… … Математическая энциклопедия
ОРТОГОНАЛЬНЫЙ РЯД — ряд вида где ортонормированная система функций (онс) относительно меры : Начиная с 18 в. при изучении различных вопросов математики, астрономии, механики и физики (движение планет, колебание струн, мембран и др.) в исследованиях Л. Эйлера (L.… … Математическая энциклопедия
ХАУСДОРФА - ЮНГА НЕРАВЕНСТВА — оценки коэффициентов Фурье функций из L р;установлены У. Юнгом [1] и Ф. Хаусдорфом [2]. Пусть ортонормированная система функций на [ а, b], для всех и всех n = 1, 2, ... и Если то где с n (f) коэффициенты Фурье функции f. Если то существует такая … Математическая энциклопедия
 скалярное произведение
скалярное произведение  , где δij — символ Кронекера.
, где δij — символ Кронекера.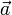 может быть вычислено по формулам:
может быть вычислено по формулам:  , где
, где  .
. образуют ортонормированную систему функций на конечном интервале [a,b] , если для них выполняется условие
образуют ортонормированную систему функций на конечном интервале [a,b] , если для них выполняется условие
 .
.