- ОБОБЩЕННОЕ РЕШЕНИЕ
- обобщение понятия классич. решений дифференциальных (псевдодифференциальных) уравнений. Это понятие возникло в связи с многими задачами математич. физики, когда под решениями дифференциальных уравнений потребовалось понимать функции, не имеющие достаточного числа производных, и даже вовсе недифференцпруемые функции, а также более общие объекты - обобщенные функции, гиперфункции и т. д. Поэтому понятие О. р. тесно связано с понятием обобщенной производной и вообще обобщенной функции.
Под обобщенным решением дифференциального уравнения

в классе
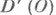 . понимается всякая обобщенная функция ииз
. понимается всякая обобщенная функция ииз 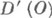 , удовлетворяющая уравнению (1) в О, т. е. для любой основной функции
, удовлетворяющая уравнению (1) в О, т. е. для любой основной функции 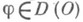 должно
должно быть выполнено равенство
 - сопряженный оператор к Lв смысле Лагранжа:
- сопряженный оператор к Lв смысле Лагранжа:
О. р. краевых задач для дифференциальных уравнений удовлетворяют краевым условиям в надлежащем обобщенном смысле (в L р( дО). или D'( дО )и т. д.), напр.:
 ),
),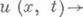

О. р. краевых задач для дифференциальных уравнений возникают при решении их вариационными методами, при применении разностных методов, а также как слабые пределы классич. решений при применении Фурье метода, предельного поглощения принципа, предельной амплитуды принципа, методов, связанных с введением вязкости, и т. д.
Примеры. 1) Общее решение уравнения
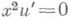 в классе
в классе  дается формулой
дается формулой
где
 - функция Хевисайда:
- функция Хевисайда:
 - дельта-функция Дирака,
- дельта-функция Дирака, 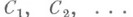 - здесь и далее произвольные постоянные.
- здесь и далее произвольные постоянные.2) Уравнение
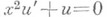 имеет одно решение в классе
имеет одно решение в классе 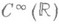 , равное
, равное 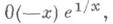 а в классе гиперфункций общее решение его дается формулой
а в классе гиперфункций общее решение его дается формулой 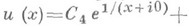

3) Общее решение волнового уравнения
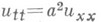 в классе
в классе  дается формулой
дается формулой 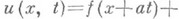
 где f и g- произвольные функции класса
где f и g- произвольные функции класса
4) Всякое решение ииз D'(0) уравнения Лапласа
 - (вещественно) аналитическое в О.
- (вещественно) аналитическое в О.5) Всякое решение ииз D' уравнения теплопроводности
 - бесконечно дифференцируемое.
- бесконечно дифференцируемое.6) Всякий дифференциальный оператор
 с постоянными коэффициентами имеет фундаментальное решение (медленного роста) из класса S'.
с постоянными коэффициентами имеет фундаментальное решение (медленного роста) из класса S'.7) Всякое уравнение
 - дифференциальный оператор с постоянными коэффициентами, имеет при любом
- дифференциальный оператор с постоянными коэффициентами, имеет при любом 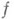 из
из  О. р. и из
О. р. и из 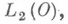 если О- ограниченная область.
если О- ограниченная область.8) О. р. икраевой задачи

в классе Соболева
 возникает как решение классической вариационной задачи о минимуме квадратичного функционала
возникает как решение классической вариационной задачи о минимуме квадратичного функционала
в классе
 . Решение этой вариационной задачи при любом f из
. Решение этой вариационной задачи при любом f из  существует и единственно в классе
существует и единственно в классе  . Таким образом, О. р. краевой задачи (2) при всех
. Таким образом, О. р. краевой задачи (2) при всех  дают самосопряженное расширение оператора
дают самосопряженное расширение оператора  (жесткое расширение, или расширение по Фридрихсу). О. р. краевой задачи (2), как и все их производные,- регулярные в О(т. е. типа локально интегрируемых функций в О), вторые их, производные, вообще говоря,- сингулярные обобщенные функции.
(жесткое расширение, или расширение по Фридрихсу). О. р. краевой задачи (2), как и все их производные,- регулярные в О(т. е. типа локально интегрируемых функций в О), вторые их, производные, вообще говоря,- сингулярные обобщенные функции.Лит.:[1] Соболев С. Л., "Матем. сб.", 1936, т. 1, № 1, с. 39-72; [2] его же, Некоторые применения функционального анализа в математической физике, Новосиб., 1962; [3] Schwartz L., Theorie des distributions, t. 1-2, P., 1950-51; [4] Гельфанд И. M, Шилов Г. Е., Некоторые вопросы дифференциальных уравнений, М., 1958; [5] Хёрмандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965; [6] Hyperfunctions and pseudo-differential eduations, В.- [u. a.], 1973; [7] Владимиров В. С, Уравнения математической физики, 4 изд., М., 1981; [8] его же, Обобщенные функции в математической физике, М., 2 изд., 1979.
В. С. Владимиров.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
