МНОЖЕСТВ КАТЕГОРИЯ

МНОЖЕСТВ КАТЕГОРИЯ

- категория, объектами к-рой являются всевозможные множества, морфиз-мами - всевозможные отображения множеств друг в друга, и умножение морфизмов определяется как последовательное выполнение отображений и Если теоретико-категорные рассмотрения проводятся внутри фиксированного универсального множества U, то под М. к. понимают категорию, объектами к-рой являются всевозможные множества, принадлежащие U, а морфизмы и их умножение вводятся, как и выше. М. к. обозначают либо 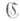, либо Ens, либо , либо Me.

Пустое множество является левым нулем (инициальным объектом), а одноэлементное множество - правым нулем (терминальным объектом) М. к. Всякое непустое множество является образующим объектом, всякое множество, содержащее не менее двух элементов,- кообразующим (коинтегральным) объектом М. к. Всякий мономорфизм с непустым началом есть обратимое справа инъективное отображение, всякий эпиморфизм есть обратимое слева сюръективное отображение. М. к. обладает единственной бикатегорной структурой.

М. к. является локально малой биполной категорией. В частности, произведение семейства множеств совпадает с декартовым произведением этого семейства, копроизведение семейства множеств совпадает с разъединенным объединением этого семейства. Декартово произведение, рассматриваемое как бифунктор, Hom-функтор и одноэлементное множество снабжают М. к. структурой замкнутой категории. Всякая категория относительная категория над М. к. Двухэлементное множество снабжает М. к. дополнительной структурой (абстрактного) топоса.

Категория тогда и только тогда эквивалентна М. к., когда в имеется- формально присоединенный левый нуль 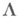, а полная подкатегория является категорией с регулярными кообразами с унарным образующим объектом, для каждого объекта Ак-рой существует произведение и каждое отношение эквивалентности

индуцировано ядерной парой нек-рого морфизма. Объект Uназ. унарным, если существуют любые копроизведения

и если всякий морфизм

представим в виде 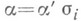для единственного i. О других характеризациях М. к. см. [2], [3].

Категории, изоморфные подкатегориям М. к., наз. конкретными. О необходимых и достаточных условиях конкретности категории см. [1].

Лит.:[1] Frеуd P., "J. Pure and Appl. Algebra", 1973, v. 3, № 2, p. 171-91; [2] Lawvere P. W., "Proc. Nat. Acad. Sci. USA", 1964, v. 52, № 6, p. 1506 - 11; [3] Скорняков Л. А., "Матем. сб.", 1969, т. 80, № 4, с. 492-502.

М. Ш. Цаленко.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем решить контрольную работу

Полезное


Смотреть что такое "МНОЖЕСТВ КАТЕГОРИЯ" в других словарях:

  • КАТЕГОРИЯ — понятие, выделяющее ряд алгебраич. свойств совокупностей морфизмов однотипных математич. объектов (множеств, топологич. пространств, групп и т. п.) друг в друга при условии, что эти совокупности содержат тождественные отображения и замкнуты… …   Математическая энциклопедия

  • Категория (математика) — Теория категорий  раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Некоторые математики[кто?] считают теорию категорий слишком абстрактной и непригодной для… …   Википедия

  • Категория Люстерника — Шнирельмана — характеристика топологического пространства X минимальное число таких замкнутых множеств, которыми можно покрыть X и каждое из которых может быть стянуто в точку посредством непрерывной деформации в X. Категория Люстерника Шнирельмана является… …   Википедия

  • Категория Люстерника—Шнирельмана — характеристика топологического пространства X минимальное число таких замкнутых множеств, которыми можно покрыть X и каждое из которых может быть стянуто в точку посредством непрерывной деформации в X. Категория Люстерника Шнирельмана является… …   Википедия

  • Категория Люстерника — Шнирельмана характеристика топологического пространства минимальное число таких замкнутых множеств, которыми можно покрыть и каждое из которых может быть стянуто в точку посредством непрерывной деформации в . Категория Люстерника Шнирельмана… …   Википедия

  • КАТЕГОРИЯ С ИНВОЛЮЦИЕЙ — категория, обладающая рядом характерных свойств категории бинарных отношений. К. с и. наз. категория, в к рой каждое множество Н( А, В )частично упорядочено отношением а также задано отображение наз. инволюцией, сопоставляющее морфизму а морфизм… …   Математическая энциклопедия

  • Категория Бэра — У этого термина существуют и другие значения, см. Бэр. Категория Бэра один из способов различать «большие» и «маленькие» множества. Подмножество топологического пространства может быть первой или второй категории Бэра. Названа в честь… …   Википедия

  • ЗАМКНУТАЯ КАТЕГОРИЯ — категория с дополнительной структурой, позволяющей использовать внутренний Hom функтор как сопряженный справа функтор к абстрактному тензорному произведению. Категория наз. замкнутой, если в ней задан бифунктор (см. Функтор), выделен объект I,… …   Математическая энциклопедия

  • КАТЕГОРИЯ МНОЖЕСТВА — топологическая характеристика массивности множества. Множество Етопологич. пространства Xназ. множеством первой категории на X, если оно представимо в виде конечной или счетной суммы множеств, нигде не плотных на X. В противном случае Еназ.… …   Математическая энциклопедия

  • КАТЕГОРИЯ — (в смысле Люстерника Шнирельмана) характеристика топологич. пространства Е минимальное число cat Е таких замкнутых множеств к рыми можно покрыть Еи каждое из к рых может быть стянуто в точку посредством непрерывной деформации в Е. К. является… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»