КАТЕГОРИЯ

- понятие, выделяющее ряд алгебраич. свойств совокупностей морфизмов однотипных математич. объектов (множеств, топологич. пространств, групп и т. п.) друг в друга при условии, что эти совокупности содержат тождественные отображения и замкнуты относительно последовательного выполнения (суперпозиции или умножения) отображений. К.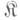состоит из класса 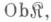элементы к-рого наз. объектами категории, и класса 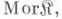элементы к-рого наз. морфизмамикатегории. Эти классы должны удовлетворять следующим условиям:

1) Каждой упорядоченной паре объектов А, В сопоставлено множество 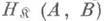(обозначаемое также Нот ( А, В )или Н( А, В ))из Мог; если 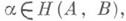то говорят, что А- начало, или область определения, морфизма а, а В - конец, или область значений а; часто вместо пишут a.: или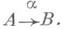

2) Каждый морфизм К. принадлежит одному и только одному множеству

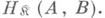
3) В классе Моrзадан частичный закон умножения: произведение морфизмов a.: и b : определено тогда и только тогда, когда В = С, и принадлежит множеству Н( А, D), произведение a и b обозначается ab или ba.

4) Для любых морфизмов a : b : и у : справедлив закон ассоциативности: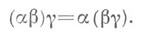

5) В каждом множестве 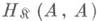содержится такой морфизм 1_A, что aХ1_A=a и 1_A Х b= b для любых морфизмов a : и b :; морфизмы 1 _А наз. единичными, тождественными, или единицами.

Входящее в определение К. понятие класс предполагает использование такой аксиоматики теории множеств, к-рая различает множества и классы. Наиболее употребительной является аксиоматика Гёделя- Бернсайда - Неймана.

Иногда в определении К. не требуют, чтобы классы Н(А, В)являлись множествами. Иногда вместо использования классов предполагается существование универсального множества и требуется принадлежность классов и фиксированному универсальному множеству.

Поскольку между единицами К.и классом имеется биективное соответствие, К. можно определить как класс морфизмов с частичным умножением, удовлетворяющим дополнительным требованиям (см., напр., [6], [9]).

Понятие К. было введено в 1945 [8]. Своим происхождением и первоначальными стимулами развития теория К. обязана алгебраич. топологии. Последующие исследования выявили объединяющую и унифицирующую роль понятия К. и связанного с ним понятия функтора для многих разделов математики.

Примеры К.:

1) Категория множеств Ens; класс Ob Ens состоит из всевозможных множеств, класс Мог Ens - из всевозможных отображений множеств друг в друга, а умножение совпадает с последовательным выполнением отображений (см. Множеств категория).

2) Категория топологических пространств Тор (или ); класс Ob Top состоит из всевозможных топологич. пространств, класс Моr Тор - из всех непрерывных отображений топологич. пространств, а умножение снова совпадает с последовательным выполнением отображений.

3) Категория групп Gr (или ); класс Ob Gr состоит из всевозможных групп, класс Мог Gr - из всех гомоморфизмов групп, а умножение опять совпадает с последовательным выполнением гомоморфизмов (см. Групп категория). По аналогии с этими примерами можно ввести К. векторных пространств над нек-рым телом, К. колец и т. п.

4) Категория бинарных отношений множеств Rel Ens (или R(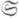)); класс объектов этой К. совпадает с классом Ob Ens, а морфизмами множества Ав множество Вслужат бинарные отношения этих множеств, т. е. всевозможные подмножества декартова произведения А В;умножение совпадает с умножением бинарных отношений.

5) Полугруппа с единицей является К. с одним объектом, и наоборот, каждая К., состоящая из одного объекта, есть полугруппа с единицей.

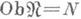6) Предупорядоченное множество Nможно рассматривать как К. для которой и 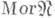={(a, b)| а,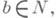}, а умножение определяется равенством (а, b)(b, с)=( а, с).

Все перечисленные выше К. допускают изоморфное вложение в К. множеств. К., обладающие указанным свойством, наз. конкретными К. Не всякая К. конкретна, напр., такова К., объектами к-рой являются все топологич. пространства, а морфизмами - классы гомотопных отображений [10].

Запас примеров К. можно значительно расширить при помощи различных конструкций и прежде всего при помощи К. функторов или К. диаграмм.

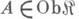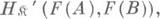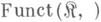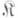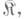Отображение F:категории в категорию наз. ковариантным функтором, если для каждого объекта объект для каждого морфизма образ F(a)причем F(1_A)=1_F(A) и F(ab)=F(a)F(b). всякий раз, когда определено произведение ab. Если объекты К. составляют множество, то можно построить К. диаграмм или объектами к-роп являются всевозможные ковариантные функторы из в а морфизмами - всевозможные естественные преобразования этих функторов.

Каждой К. может быть сопоставлена двойственная, или дуальная, К.. или 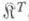, для которо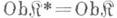й и для любых Ковариантный функтор из в наз. контравар и антным функтором из в 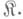Наряду с функторами одного аргумента можно рассматривать многоместные функторы или функторы от многих аргументов.

Для каждого предложения теории К. существует двойственное (дуальное) предложение, к-рое получается формальным "обращением стрелок". При этом справедлив так наз. принцип двойственности: предложение ристинно в теории К. тогда и только тогда, когда в этой теории истинно двойственное предложение р*.

Многие понятия и результаты в математике оказались двойственными друг другу с категорной точки зрения: инъективность и проективность, нильпотентность и К. топологич. пространства в смысле Люстерника - Шнирельмана, многообразия и радикалы в алгебре и т. д.

Теоретико-категорный анализ основ теории гомологии привел к выделению в середине 50-х гг. 20 в. так наз. абелевых категорий, в рамках к-рых оказалось возможным осуществить основные построения гомологич. алгебры [2]. В 60-е гг. 20 в. определился возрастающий интерес к неабелевым К., вызванный задачами логики, общей алгебры, топологии и алгебраич. геометрии. Интенсивное развитие универсальной алгебры и аксиоматич. построения теории гомотопий положили начало различным направлениям исследований: категорному изучению многообразий универсальных алгебр, теории изоморфизмов прямых разложений, теории сопряженных функторов и теории двойственности функторов. Последующее развитие обнаружило существенные взаимосвязи между этими исследованиями. Благодаря возникшей в последние годы теории относительных К., широко использующей технику сопряженных функторов и замкнутых К., была установлена двойственность между теорией гомотопий и теорией универсальных алгебр, основанная на интерпретации категорных определений моноида и комоноида в подходящих К. функторов (см., напр., [7]). Наряду с развитием общей теории относительных К., шло выделение специальных классов таких К.: 2-категории, или формальные К., К. с инволюцией, или 1-категории, включающие, в частности, К. бинарных отношений, и т. д. В частности, 2-категорией является К. малых К., к-рая может быть положена в основу аксиоматического построения математики.

Перечисленные классы К. характеризуются тем, что их множестваморфизмов Н( А, В )обладают дополнительной структурой. Другой способ введения дополнительных структур в К. связан с заданием в К. топологии и построении К. пучков над топологизированной К. (так наз. топосы).

Лит.:[1] Бувур И., Деляну А., Введение в теорию категорий и функторов, пер. с англ., М., 1972; [2] Гротендик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961; [3] Курош А. Г., Лившиц А. X., Шульгейфер Е. Г., "Успехи матем. наук", 1960, т. 15, в.6, с. 3-52; [4] Итоги науки. Алгебра. Топология. 1962, М., 1963,,с. 90-106; [5] Итоги науки. Алгебра. Топология. Геометрия. 1967, М., 1969, с. 9-57; [6] Цаленко М. Ш., Шульгейфер Е. Г., Основы теории категорий, М., 1974; [7] Bunge M., "J. Algebra", 1969, v. 11, р. 64-101; [8] Еilenberg S., М а с Lane S., "Trans. Amer. Math. Soc", 1945, v. 58, P. 231-94; [9] Freyd P., Abelian categories, N. Y., 1964; [10] его же, "Symposia mathem.", IV, S. 431 - 56; [11] Mас Lane S., Kategorien. Begriffssprache und mathematische Theorie, В., 1972; [12] Schubert H., Kategorien, Bd 1-2, В., 1970; [13] Mitchell В., Theory of categorie, N. Y., 1965.

M. Ш. Цаленко.