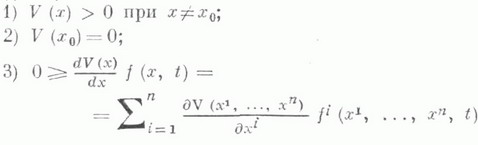ЛЯПУНОВА ТЕОРИЯ УСТОЙЧИВОСТИ — теория устойчивости движения, построенная А. М. Ляпуновым в конце 19 нач. 20 вв. (см. [1]). В основе ее лежат понятия устойчивости по Ляпунову и асимптотич. устойчивости (см. Асимптотически устойчивое решение),введенные А. М. Ляпуновым, теорема… … Математическая энциклопедия
Функция Ляпунова — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. В теории обыкновенных дифференциальных уравнений, функция Ляпунова является скалярной функцией, которая… … Википедия
ЛЯПУНОВА СТОХАСТИЧЕСКАЯ ФУНКЦИЯ — неотрицательная функция V(t, х), для к рой пара (V(t, X(t)), Ft) супермартингал для нек рого случайного процесса X(t), Ft есть s алгебра событий, порожденных течением процесса Xдо момента t. Если X(t) марковский процесс, то Л. с. ф. есть функция … Математическая энциклопедия
функция Ляпунова — Liapunovo funkcija statusas T sritis automatika atitikmenys: angl. Lyapunov function vok. Ljapunov Funktion, f rus. функция Ляпунова, f pranc. fonction de Lyapunov, f … Automatikos terminų žodynas
ЛЯПУНОВА - ШМИДТА УРАВНЕНИЕ — нелинейное интегральное уравнение вида где неотрицательные целые числа, ограниченное замкнутое множество конечномерного евклидова пространства, v и функции К заданные непрерывные функции своих аргументов и искомая функция … Математическая энциклопедия
ГРИНА ФУНКЦИЯ — функция, связанная с интегральным представлением решений краевых задач для дифференциальных уравнений. Г. ф. краевой задачи для линейного дифференциального уравнения фундаментальное решение уравнения, удовлетворяющее однородным краевым условиям.… … Математическая энциклопедия
ОБОБЩЕННАЯ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ — функция удовлетворяющая системе с действительными коэффициентами являющимися функциями действительных переменных хи у В обозначениях исходная система записывается в виде Если коэффициенты Аи Всистемы (1) на всей плоскости Екомплексного… … Математическая энциклопедия
ЧЕТАЕВА ФУНКЦИЯ — функция v(x) и окрестности неподвижной точки х =0 системы обыкновенных дифференциальных уравнений обладающая двумя свойствами: 1) существует примыкающая к точке x=0 область G, в к рой v>0, и v=0 на границе области Gвблизи x=0; 2) в области… … Математическая энциклопедия
Центральная предельная теорема Ляпунова — Центральные предельные теоремы (Ц.П.Т.) класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях… … Википедия
векторная функция Ляпунова — vektorinė Liapunovo funkcija statusas T sritis automatika atitikmenys: angl. Lyapunov vector function vok. Ljapunovsche Vektorfunktion, f rus. векторная функция Ляпунова, f pranc. fonction vectorielle de Lyapunov, f … Automatikos terminų žodynas
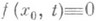), где отображение 
непрерывной непрерывно дифференцируемо по х(здесь U - нек-рая окрестность точки х 0 в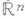 
); в координатах эта система записывается в виде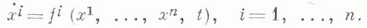 
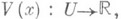обладающая свойствами:
