ЛИ АЛГЕБРА АЛГЕБРАИЧЕСКОЙ ГРУППЫ

- аналог Ли алгебры аналитической группы, относящийся к случаю аффинных алгебраич. групп. Как и в аналитич. случае, Ли а. а. г. Gесть касательное пространство к б в единице, а структура алгебры Ли определена в нем с помощью левоинвариантных дифференцирований алгебры функций на G. Точное определение состоит в следующем.

Пусть К - алгебраически замкнутое поле, G - аффинная алгебраич. К-группа, - алгебра регулярных функций на G и Lie (G) - множество всех дифференцирований К-алгебры А, к-рые коммутируют с автоморфизмами алгебры А, определенными левыми сдвигами из G. Пространство Lie (G) является алгеброй Ли с операцией (см. Ли линейная алгебра), а операция (рсомножителей) определяет на Lie (G) структуру р-алгебры Ли (рравно характеристике поля К, если она положительна, и равно 1, если она нулевая). Пусть L(G) - касательное пространство к G в единице е, т. е. векторное пространство над Квсех К-дифференцирований из Ав A-модуль где - максимальный идеал точки е, и пусть 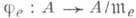канонич. гомоморфизм. Для любого 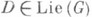композиция является элементом из L(G), а отображение определенное формулой является изоморфизмом векторных пространств над К. Это позволяет перенести с Lie (G) на L(G) структуру р-алгебры Ли. Эта р-алгебра Ли L(G) и наз. Ли а. а. г. G. Если k - подполе в Ки G определена над k, то левоинвариантные k-дифференцирования k-алгебры определяющей k-структуру на G, образуют k-структуру на Lie(G), а указанный выше изоморфизм определен над k.

Пример. Пусть V- конечномерное векторное пространство над Ки G = GL(V).- алгебраич. группа всех автоморфизмов пространства V. Тогда касательное пространство к G в точке еестественно отождествляется с векторным пространством End Vвсех эндоморфизмов пространства V, а структура Ли а. а. г. С на End Vзадается формулами: [X, Y] = XY - YX, Полученная алгебра Ли обозначается

Ли а. а. г. обладают рядом свойств, аналогичных свойствам алгебр Ли аналитич. рупп. Так, дифференциал гомоморфизма алгебраич. групп в единице есть гомоморфизм их алгебр Ли. Размерность Ли а. а. г. G равна размерности группы G. Ли а. а. г. G и ее связной компоненты единицы совпадают. Дифференциал присоединенного представления алгебраич. группы является присоединенным представлением ее алгебры Ли. Если Н - алгебраич. подгруппа в алгебраич. группе G, то L(Н).есть подалгебра в L(G). Более того, пусть J- идеал всех регулярных функций на G, обращающихся в нуль на Н. Тогда, отождествляя L(G).с Lie (G), можно описать L(H).как множество всех таких элементов из Lie(G), к-рые аннулируют J. Это описание особенно удобно при рассмотрении линейных алгебраич. групп, т. е. алгебраич. подгрупп G в GL(V). А именно, пусть J - идеал JC[End V], состоящий из элементов, равных нулю на G. Тогда состоит в точности из таких эндоморфизмов Xпространства V, что дифференцирование алгебры К[End V], порожденное эндоморфизмом пространства End V, переводит J в себя. Операции же в L(G).индуцированы описанными выше операциями в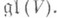

Если р=1, то связь между аффинными алгебраич. группами и их алгебрами Ли является по существу столь же тесной, как связь между аналитич. руппами и их алгебрами Ли. Это позволяет в значительной степени сводить изучение аффинных алгебраич. групп к изучению их алгебр Ли и обратно. При этом алгебры Ли линейных алгебраич. групп (т. е. алгебраич. подгрупп в GL(V)) выделяются среди всех подалгебр Ли в с помощью внутреннего критерия (см. Ли алгебраическая алгебра). В случае р > 1 указанная связь не является столь тесной и в значительной степени теряет свое значение. А именно, в этом случае в общем справедливыми остаются лишь результаты, позволяющие извлекать из свойств группы сведения о свойствах ее алгебры Ли. Напротив, многие теоремы, устанавливающие в случае р=1 эту связь в обратную сторону, перестают быть справедливыми. Напр., могут существовать различные связные подгруппы данной группы, алгебры Ли к-рых совпадают; алгебра Ли неразрешимой алгебраич. группы может быть разрешимой (это так, напр., для группы матриц порядка 2 с определителем 1 при p=2) и т. п.

Лит.:[1] Б о р е л ь А., Линейные алгебраические группы, пер. с англ., М., 1972; [2] Ш е в а л л е К., Теория групп Ли, пер. о франц., т. 2, М., 1958. В. Л. Попов.