ЛЕФШЕЦА ЧИСЛО

- инвариант отображения цепного (коцепного) комплекса или топологич. пространства в себя. Пусть X - цепной комплекс абелевых групп (соответственно топологич. пространство), f: - эндоморфизм степени 0 (соответственно непрерывное отображение), - гомологии группы, объекта Xс коэффициентами в поле рациональных чисел 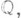причем

и пусть t_i - след линейного преобразования

По определению, число Лефшеца отображения f есть

В случае коцепного комплекса определение аналогично. В частности, Л. ч. тождественного отображения е _X равно эйлеровой характеристике 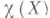объекта X. Если X - цепной (коцепной) комплекс свободных абелевых групп или топологич. пространство, то число всегда целое. Л. ч. было введено С. Лефшецем [1] для решения задачи о числе неподвижных точек непрерывного отображения (см. Лефшеца формула). Для нахождения Л. ч. эндоморфизма f комплекса X, состоящего из конечномерных векторных пространств Xнад можно воспользоваться следующей формулой (к-рая иногда наз. формулой следа X о п ф а)

где Т,- - след линейного преобразования 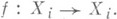В частности, если X - конечное клеточное пространство, - его непрерывное отображение в себя и 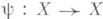- нек-рая клеточная аппроксимация отображения ф, то

где Т _i - след преобразования

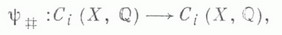
индуцированного отображением а - группа рациональных _i -мерных цепей клеточного пространства X.

Все сказанное выше допускает обобщение на случай произвольного поля коэффициентов.

Лит.:[1]Lefschetz S., "Trans Amer. Math. Soc.", 1926, v. 28, p. 1 - 49; [2] 3 e й ф e р т Г., Т р е л ь ф а л л ьВ., Топология, пер. с нем.. М.- Л., 1938. Ю. Б. Рудяк.