- КЭЛИ - ДИКСОНА АЛГЕБРА
- альтернативная 8-мерная алгебра, получающаяся из алгебры обобщенных кватернионов применением процесса Кэл и- Диксона. Этот процесс заключается в построении по заданной алгебре Ановой алгебры А 1 (удвоенной размерности) и является обобщением процесса удвоения (см. Гиперкомплексное число). А именно, пусть А- алгебра с единицей 1 над нолем F,d - некоторый ненулевой элемент из Fи задано F-линейное отображение
 являющееся инволюцией, причем
являющееся инволюцией, причем
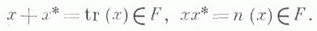
На прямой сумме линейных пространств
 формулой
формулой  определяется умножение, превращающее А 1 в алгебру. Алгебра Авкладывается в А 1 в качестве подалгебры:
определяется умножение, превращающее А 1 в алгебру. Алгебра Авкладывается в А 1 в качестве подалгебры: 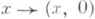 и инволюция * продолжается до инволюции в А 1:
и инволюция * продолжается до инволюции в А 1:

При этом

Процесс перехода от алгебры Ак алгебре А 1 можно продолжить, получая возрастающую цепочку алгебр
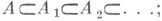 параметр d на каждом шаге может меняться. Если процесс Кэли - Диксона начинается с алгебры Ас базисом {1, и},таблицей умножения
параметр d на каждом шаге может меняться. Если процесс Кэли - Диксона начинается с алгебры Ас базисом {1, и},таблицей умножения
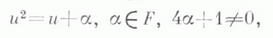
и инволюцией:
 то после первого шага получится алгебра A1 обобщенных кватернионов (ассоциативная алгебра размерности 4), а на втором шаге - алгебра А 2 размерности 8, к-рая и наз. К э л и-Д и к с о н а алгеброй.
то после первого шага получится алгебра A1 обобщенных кватернионов (ассоциативная алгебра размерности 4), а на втором шаге - алгебра А 2 размерности 8, к-рая и наз. К э л и-Д и к с о н а алгеброй.
Любая К.- Д. а. является альтернативной, но не ассоциативной центральной простой алгеброй над F;обратно, простое альтернативное кольцо либо ассоциативно, либо является К.- Д. а. над своим центром. Определенная на К.-Д. а. квадратичная форма (х).от восьми переменных, соответствующих базису алгебры, обладает мультипликативным свойством:

Тем самым устанавливается связь между К.- Д. а. и проблемой существования композиции для квадратичных форм. К.- Д. а. является алгеброй с делением тогда и только тогда, когда квадратичная форма (х).(норма э л е м е н т а х).не представляет нуля в F. Если характеристика поля Fотлична от 2, то К.- Д. а. обладает базисом
 с таблицей умножения вида
с таблицей умножения вида

где
 а инволюция определяется условиями
а инволюция определяется условиями 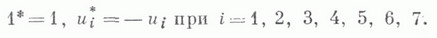
Эта алгебра обозначается
 Алгебры
Алгебры 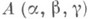 и
и  изоморфны тогда и только тогда, когда эквивалентны отвечающие им квадратичные формы (х). Если (х).представляет нуль, то соответствующая К.- Д. а. изоморфна А(-1, 1, 1). Алгебра (-1, 1, 1) наз. расщепляемой алгеброй К э л и, или векторно-матричной алгеброй. Ее элементы могут быть представлены матрицами вида
изоморфны тогда и только тогда, когда эквивалентны отвечающие им квадратичные формы (х). Если (х).представляет нуль, то соответствующая К.- Д. а. изоморфна А(-1, 1, 1). Алгебра (-1, 1, 1) наз. расщепляемой алгеброй К э л и, или векторно-матричной алгеброй. Ее элементы могут быть представлены матрицами вида

где
 - трехмерное пространство над Fс обычными операциями скалярного произведения
- трехмерное пространство над Fс обычными операциями скалярного произведения  и векторного произведения
и векторного произведения 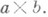 Умножение этих матриц задается формулой
Умножение этих матриц задается формулой

Если
 - поле действительных чисел, то A (1, 1, 1) - алгебра Кэли чисел (она является алгеброй с делением). Любая К.- Д. а. над
- поле действительных чисел, то A (1, 1, 1) - алгебра Кэли чисел (она является алгеброй с делением). Любая К.- Д. а. над  изоморфна либо А(1,1, 1), либо А(-1, 1, 1). Построение К.- Д. а. над произвольным полем принадлежит Л. Диксону (L. Dickson), к-рый изучил также их основные свойства (см. [1], [2]). Пусть А- альтернативное кольцо, ассоциативно-коммутативный центр Ск-рого отличен от нуля и не содержит делителей нуля, a F - поле частных кольца С. Тогда имеется естественное вложение
изоморфна либо А(1,1, 1), либо А(-1, 1, 1). Построение К.- Д. а. над произвольным полем принадлежит Л. Диксону (L. Dickson), к-рый изучил также их основные свойства (см. [1], [2]). Пусть А- альтернативное кольцо, ассоциативно-коммутативный центр Ск-рого отличен от нуля и не содержит делителей нуля, a F - поле частных кольца С. Тогда имеется естественное вложение 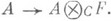 Если
Если 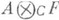 есть К.- Д. а. над F, то Аназ. кольцом Кэли - Диксона.
есть К.- Д. а. над F, то Аназ. кольцом Кэли - Диксона.
Лит.:[1] Д и к с о н Л. Э., Линейные алгебры, пер. с англ., Харьков, 1935; [2] Schafer R. D., An introduction, to nonassociative algebras, N. Y., 1966; [3] Ж е в л а к о в К. А., Слинько А. М., Шестаков И. П., Ширшов А. И., Кольца, близкие к ассоциативным, М., 1978. Е. Н. Кузьмин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
