ЛИ ОСОБАЯ АЛГЕБРА

- простая алгебра Ли (см. Ли полупростая алгебра), не являющаяся классической. Над алгебраически замкнутым полем нулевой характеристики существует всего 5 Ли о. а.: Е ₆, Е ₇, E₈, F₄ н G₂ размерностей 78, 133, 248, 52 и 14 соответственно. Индексы в обозначениях равны рангам этих алгебр Ли. Простейшие линейные представления этих Ли о. а. имеют размерности 27, 56, 248, 26 и 7 соответственно. Алгебра G₂ есть алгебра дифференцирований Кэли-Диксона алгебры,a F₄- алгебра дифференцирований единственной особой йорданоеой алгебры, к-рую можно представить как алгебру эрмитовых матриц третьего порядка над алгеброй Кэли-Диксона. Алгебра E₆ есть линейная оболочка дифференцирований и умножений на элементы особой йордановой алгебры. Алгебры Е ₇, и Е ₈ и формы всех Ли о. а. над алгебраически незамкнутыми полями также связаны с алгеброй Кэли - Диксона. Различные модели Ли о. а. получаются при рассмотрении их градуировок посредством циклич. групп. Связные группы Ли, соответствующие Ли о. а., наз. особыми группами Ли и часто обозначаются теми же буквами. Напр., комплексная группа G₂- это группа автоморфизмов алгебры Кэли- Диксона над 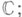комплексная группа F₄- это группа автоморфизмов особой йордановой алгебры над С.

Лит.:[11 Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] е г о же, Exceptional Lie Algebras, N. Y., 1971; [3] Фрейденталь Г., "Математика", 1957, т. 1, № 1, с. 117-53; [4] Р о з е н ф е л ь д Б. А., в кн.: Algebraical and Topological Foundations of Geometry, Oxf.- [a. o.l, 1962, p. 135-55; [5] В и н б е р г Э. Б., в кн.: Тр. Семинара по векторному и тензорному анализу..., в. 13, М., 1966, с. 7-9; [6] Tits J., "Judag. Math.", 1966, v. 28, X°2, p. 223-37; [71 его же, Tabellen zu den einfaclien Lie Gruppen und ihren Dar-stellungen, В.- [u. a.], 1967. Э. Б. Винберг.