коядро — сущ., кол во синонимов: 1 • ядро (52) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
АБЕЛЕВА КАТЕГОРИЯ — категория, обладающая рядом характерных свойств категории всех абелевых групп. А. к. были введены как основа абстрактного построения гомологич. алгебры (см. [4]). Категория наз. абелевой (см. [2]), если она удовлетворяет следующим аксиомам: А0.… … Математическая энциклопедия
МНОГООБРАЗИЕ — категорий понятие, аналогичное понятию многообразия универсальных алгебр. Пусть бикатегория с произведениями. Полная подкатегория категории наз. многообразием, если она удовлетворяет следующим условиям: а) если допустимый мономорфизм и б) если… … Математическая энциклопедия
ТОПОЛОГИЯ — в широком смысле область математики, изучающая топологич. свойства разл. матем. и физ. объектов. Интуитивно, к топологич. относятся качественные, устойчивые свойства, не меняющиеся при деформациях. Матем. формализация идеи о топологич. свойствах… … Физическая энциклопедия
АДДИТИВНАЯ КАТЕГОРИЯ — категория С, в к рой для любых двух объектов на множестве морфиз мов определена структура абелевой группы таким образом, что композиция морфизмов является билинейным отображением. Кроме того, требуется, чтобы в Ссуществовал нулевой объект (или… … Математическая энциклопедия
ВЕЙЛЯ - ШАТЛЕ ГРУППА — группа главных однородных пространств над абелевым многообразием. То, что для любого абелева многообразия Анад полем k множество главных однородных пространств над А, определенных над k, обладает групповой структурой, было доказано А. Вейлем [1] … Математическая энциклопедия
ВЕКТОРНОЕ РАССЛОЕНИЕ — локально тривиальное расслоение : , каждый слои к рого наделен структурой (конечномерного) векторного пространства над телом ; наз. размерностью В. р. Сечения В. р. я образуют локально свободный модуль над кольцом непрерывных функций на Всо… … Математическая энциклопедия
КЕРВЕРА ИНВАРИАНТ — инвариант почти параллелизуемого гладкого многообразия Мразмерности 4k 2, определяемый как arf инвариант квадратичной формы по модулю 2, возникающий на решетке (2k+1) мерных гомологии многообразия М. Пусть М односвязное почти параллелизуемое… … Математическая энциклопедия
ЛИНЕЙНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР — в узком смысле оператор, действующий на функции, заданные на открытом множестве и принимающий значения в поле или по формуле где функции со значениями в том же поле, наз. коэффициентами А. Если коэффициенты принимают значения во множестве матриц… … Математическая энциклопедия
ЛИНЕЙНЫЙ ОПЕРАТОР — линейное преобразование, отображение между двумя векторными пространствами, согласованное с их линейными структурами. Точнее, отображение где Еи F векторные пространства над полем k, наз. л и н е й н ы м оператором из Ев F, если при всех… … Математическая энциклопедия
- категория с нулевыми морфизмами. Морфизм 
наз. коядром морфизма 
если 
и всякий морфизм 
для к-рого 
однозначно представим в виде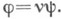 
К. морфизма 
обозначается 
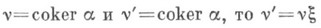для единственного изоморфизма 
- изоморфизм, то 
есть К. морфизма а. Таким образом, все К. морфизма а образуют факторобъект объекта В, к-рый обозначается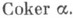 
Если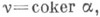 
то v - нормальный эпиморфизм. Обратное, вообще говоря, неверно. К. нулевого морфизма 
равно 
К. единичного морфизма 1A существует тогда и только тогда, когда в 
имеется нулевой объект.
с нулевым объектом морфизм 
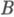обладает К. в том и только в том случае, когда в 
существует коуниверсальный квадрат относительно морфизмов 
Это условие выполнено, в частности, для любого морфизма локально малой справа категории с нулевым объектом и произведениями.