- КЕРВЕРА ИНВАРИАНТ
- инвариант почти параллелизуемого гладкого многообразия Мразмерности 4k-2, определяемый как arf-инвариант квадратичной формы по модулю 2, возникающий на решетке (2k+1)-мерных гомологии многообразия М.
Пусть М- односвязное почти параллелизуемое замкнутое гладкое многообразие размерности 4k+2, гомологич. группы Н i (М; Z )к-рого при 0<i<4k+2, кроме V=H2k+1(M; Z), равны нулю.
На свободной абелевой группе Vимеется кососимметрическая форма пересечения циклов Ф( х, у), Ф :
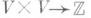 и размерность целочисленной решетки Vравна 2т. На группе V существует функция Ф 0 :
и размерность целочисленной решетки Vравна 2т. На группе V существует функция Ф 0 : определяемая следующим образом: если
определяемая следующим образом: если  то существует гладкое вложение сферы S2k+l в М, реализующее данный элемент х,
то существует гладкое вложение сферы S2k+l в М, реализующее данный элемент х, . Трубчатая окрестность этой сферы S2k+1 в Мпараллелизуема, она может быть либо тривиальной, либо изоморфной трубчатой окрестности диагонали в произведении S2k+1
. Трубчатая окрестность этой сферы S2k+1 в Мпараллелизуема, она может быть либо тривиальной, либо изоморфной трубчатой окрестности диагонали в произведении S2k+1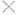 S2k+1. При этом трубчатая окрестность диагонали в S2k + 1
S2k+1. При этом трубчатая окрестность диагонали в S2k + 1 X S2k+1 тогда и только тогда нетривиальна, когда 2k+1
X S2k+1 тогда и только тогда нетривиальна, когда 2k+1 1, 3, 7 (см. Хопфа инвариант). Значение функции Ф 0 равно нулю или единице в зависимости от тривиальности или нетривиальности трубчатой окрестности сферы S2k+1, реализующей элемент хв М,2k+1
1, 3, 7 (см. Хопфа инвариант). Значение функции Ф 0 равно нулю или единице в зависимости от тривиальности или нетривиальности трубчатой окрестности сферы S2k+1, реализующей элемент хв М,2k+1 1, 3, 7. Так определенная функция Ф 0 :
1, 3, 7. Так определенная функция Ф 0 :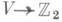 удовлетворяет свойству
удовлетворяет свойству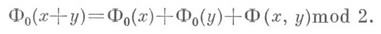
arf-инвариант для функции Ф 0 и наз. инвариантом Кервера многообразия M4k+2,

Если К, и. многообразия M4k + 2 равен нулю, то существует симплектич. базис (ei, fi) для Vтакой, что Ф 0(ei)=Ф 0(fi)=0. В этом случае многообразие M4k+2 есть связная сумма произведения сфер

Если же К. и. многообразия M4k+2 не равен нулю, то существует симплектич. базис (ei, fi) для Vтакой, что Ф 0(ei) = Ф 0(fi) = 0 для
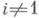 и Ф 0(e1) = Ф 0(f1)=1. В этом случае объединение трубчатых окрестностей двух (2k+1)-мерных сфер, вложенных в M4k+2 с трансверсальным пересечением в одной точке и реализующих элементы e1, f1, дает нек-рое многообразие K4k+2, наз. многообразием Кервера (см. Древовидное многообразие);его край дK4k + 2 диффеоморфен стандартной сфере, а само многообразие M4k+2 представляет собой связную сумму
и Ф 0(e1) = Ф 0(f1)=1. В этом случае объединение трубчатых окрестностей двух (2k+1)-мерных сфер, вложенных в M4k+2 с трансверсальным пересечением в одной точке и реализующих элементы e1, f1, дает нек-рое многообразие K4k+2, наз. многообразием Кервера (см. Древовидное многообразие);его край дK4k + 2 диффеоморфен стандартной сфере, а само многообразие M4k+2 представляет собой связную сумму
где гладкое замкнутое многообразие
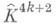 получено из K4k+2 добавлением клетки.
получено из K4k+2 добавлением клетки.Если M4k+2,
 .1, 3, есть гладкое параллелизуемое (2k)-связное многообразие с краем, к-рый является гомотопич. сферой, то точно так же определен К. и. многообразия M4k+2 с теми же свойствами, что и выше, с той разницей, что в разложении M4k+2 в связную сумму простейших многообразий слагаемое
.1, 3, есть гладкое параллелизуемое (2k)-связное многообразие с краем, к-рый является гомотопич. сферой, то точно так же определен К. и. многообразия M4k+2 с теми же свойствами, что и выше, с той разницей, что в разложении M4k+2 в связную сумму простейших многообразий слагаемое  являющееся многообразием Кервера, будет иметь край dK4k+2=dM4k+2 (вообще говоря, не диффеоморфный стандартной сфере).
являющееся многообразием Кервера, будет иметь край dK4k+2=dM4k+2 (вообще говоря, не диффеоморфный стандартной сфере).В случае k = 0, 1, 3 исходные многообразия М 2, M6, М 14 представляют собой связную сумму (S2k+1
 XS2k+1)
XS2k+1) (S2k+1XS2k+1) (если край пуст), или (S2k+1
(S2k+1XS2k+1) (если край пуст), или (S2k+1 S2k+1)o
S2k+1)o {S2k+1
{S2k+1 S2k+1)1
S2k+1)1 (S2k+1
(S2k+1 XS2k+1)m-1, (если край непуст), где (S2k+1XS2k+1)0 получено выкидыванием открытой клетки из многообразия S2k+1
XS2k+1)m-1, (если край непуст), где (S2k+1XS2k+1)0 получено выкидыванием открытой клетки из многообразия S2k+1 S2k+1.
S2k+1.Однако К. и. для замкнутых многообразий М 2, M6, М и может быть все же определен (см. Понтрягина инвариант, Кервера- Милнора инвариант )и зависит в этих размерностях от выбора оснащения, т. е. является инвариантом оснащенных перестроек пары (M4k+2, fr),k = 0,1, 3. В размерностях
 многообразие Mik + 2 тогда и только тогда перестраивается до сферы S4k+2, когда пара (M4k+2, fr). оснащенно перестраивается до пары (S4k+2, fr) при любом выборе оснащения fr на исходном многообразии M4k+2 (см. Перестройка на многообразии).
многообразие Mik + 2 тогда и только тогда перестраивается до сферы S4k+2, когда пара (M4k+2, fr). оснащенно перестраивается до пары (S4k+2, fr) при любом выборе оснащения fr на исходном многообразии M4k+2 (см. Перестройка на многообразии).К. и. определен для любого стабильно параллелизуемого многообразия M4k+2 как инвариант оснащенных перестроек и любой элемент в стабильных гомотопич. группах сфер может быть представлен либо гомотопич. сферой с оснащением, либо замкнутым гладким многообразием Кервера с оснащением (в этом случае m=4k+2,
 1, 3), либо многообразием S2k+1
1, 3), либо многообразием S2k+1 S2k+1 с оснащением, если k = 0,1, 3.
S2k+1 с оснащением, если k = 0,1, 3.Иначе говоря, К. и. можно рассматривать как препятствие к тому, чтобы заданное оснащение на многообразии "перенести" на сферу той же размерности,
 В этом смысле К. и. для значений k=0, 1, 3 выполняет ту же роль: заданное оснащение на многообразии s2k+1
В этом смысле К. и. для значений k=0, 1, 3 выполняет ту же роль: заданное оснащение на многообразии s2k+1 S2k+1, k=0, 1, 3, вообще говоря, не всегда может быть "перенесено" на сферу S4k+2, k=0, 1, 3, с помощью оснащенных перестроек.
S2k+1, k=0, 1, 3, вообще говоря, не всегда может быть "перенесено" на сферу S4k+2, k=0, 1, 3, с помощью оснащенных перестроек.Впервые такое оснащение на многообразии S2k+1
 S2k+1 было построено Л. С. Понтрягиным для случая к = 0, т. е. оснащение на двумерном торе ((S1
S2k+1 было построено Л. С. Понтрягиным для случая к = 0, т. е. оснащение на двумерном торе ((S1 S1),/ г), которое нельзя "перенести" на S2. Существуют такие же примеры оснащения на многообразиях S3
S1),/ г), которое нельзя "перенести" на S2. Существуют такие же примеры оснащения на многообразиях S3 S3 и S7
S3 и S7 S7.
S7.Основная задача, касающаяся К. и., заключается в следующем: для каких нечетных значений псуществует пара (M2n, fr )с отличным от нуля К. и.? Ответ на этот вопрос отрицателен для п
 2i-1 и положителен для п = 2i-1, где i=l (Л. С. Понтрягин, см. [2]), i=2, 3 (М. Кервер - Дж. Милнор, [5], [6]), i=4 (У. Браудер, [3]), i=5,6 [М. Баррат (М. Barratt), Maховальд (М. Mahowald), А. Мильграм (A. Milgram)]. Для остальных значений iответ неизвестен (1978).
2i-1 и положителен для п = 2i-1, где i=l (Л. С. Понтрягин, см. [2]), i=2, 3 (М. Кервер - Дж. Милнор, [5], [6]), i=4 (У. Браудер, [3]), i=5,6 [М. Баррат (М. Barratt), Maховальд (М. Mahowald), А. Мильграм (A. Milgram)]. Для остальных значений iответ неизвестен (1978).Лит.:[1] Новиков С. П., "Изв. АН СССР. Сер. матем.", 1964, т. 28, № 2, с. 365-474; [2] Понтрягин Л. С, Гладкие многообразия и их применения в теории гомотопий, 2 изд., М., 1976; [3] Вrоwder W., "Ann. Math.", 1969, v. 90, p. 157-86; [4] eго же, Surgery on simply-connected manifolds, В., 1972; [5] Кervairе М., "Comm. math, helv.", 1960, v. 34, p. 257-70; [6] Кervaire M. A., Mi1nоr J. W., "Ann. Math.", 1963, v. 77, № 3, p. 504-37.
M. А. Штанъпо.
KEPBEPA - МИЛНОРА ИНВАРИАНТ - инвариант оснащенных перестроек замкнутого 6- или 14-мерного многообразия с заданным на нем оснащением.
Пусть М 6- стабильно параллелезуемое 2-связное многообразие, на к-ром задано стабильное N-мерное оснащение ( М 6, U), т. е. тривиализация стабильного N-мерного нормального расслоения. Пусть
 - сферы, реализующие базис 3-мерных гомологии многообразия М 6. Суммированием заданной N-тривиализации Uс некоторыми тривиализациями
- сферы, реализующие базис 3-мерных гомологии многообразия М 6. Суммированием заданной N-тривиализации Uс некоторыми тривиализациями 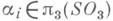 трубчатых окрестностей сфер S3 в М в получаются (N+3)-мерные тривиализации стабильных нормальных расслоений к сферам S3. и возникают элементы
трубчатых окрестностей сфер S3 в М в получаются (N+3)-мерные тривиализации стабильных нормальных расслоений к сферам S3. и возникают элементы 
 Коядро гомоморфизма стабилизации
Коядро гомоморфизма стабилизации  изоморфно Z2 для n=3, так что каждой сфере S3. сопоставляется элемент из группы p3(SON+3)/Ims (по значению элементов a1i, к-рое они принимают в группе Z2 после факторизации по а 1.). Это значение не зависит от выбора элементов ai, а зависит только от классов гомологии, реализуемых сферами S3i, и оснащения U. arf-инвариант получающейся функции
изоморфно Z2 для n=3, так что каждой сфере S3. сопоставляется элемент из группы p3(SON+3)/Ims (по значению элементов a1i, к-рое они принимают в группе Z2 после факторизации по а 1.). Это значение не зависит от выбора элементов ai, а зависит только от классов гомологии, реализуемых сферами S3i, и оснащения U. arf-инвариант получающейся функции 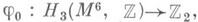 обладающей свойством j0(x+у)=j0(x)+j0(y)+j(x, y)mod 2, где j(x, у) - форма пересечений 3-мерных гомологии на многообразии М 6, и наз. инвариантом Кервера - Милнора этого многообразия с оснащением U. Пара (M6, U). оснащенно перестраивается до пары (S6, V )тогда и только тогда, когда К.- М. и. пары ( М 6, U )равен нулю.
обладающей свойством j0(x+у)=j0(x)+j0(y)+j(x, y)mod 2, где j(x, у) - форма пересечений 3-мерных гомологии на многообразии М 6, и наз. инвариантом Кервера - Милнора этого многообразия с оснащением U. Пара (M6, U). оснащенно перестраивается до пары (S6, V )тогда и только тогда, когда К.- М. и. пары ( М 6, U )равен нулю.Аналогичные построения проводятся и для М 14. К.- М. и. в размерности шесть является единственным инвариантом стабильного 6-мерного оснащенного кобордизма и задает изоморфизм
 в размерности же четырнадцать это - не единственный инвариант стабильного четырнадцатимерного оснащенного кобордизма, т. е. стабильная группа pn+14(Sn),
в размерности же четырнадцать это - не единственный инвариант стабильного четырнадцатимерного оснащенного кобордизма, т. е. стабильная группа pn+14(Sn), 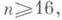 определяется оснащениями на сфере S14 и оснащениями на
определяется оснащениями на сфере S14 и оснащениями на 
Лит. см. при статье Кервера инвариант.
М. А. Штанъпо.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
