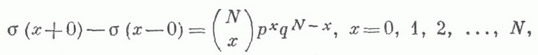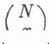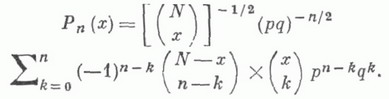Многочлены Эрмита — Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия
Многочлены Полачека — Многочлены Полачека последовательность многочленов , которые были рассмотрены Полачеком в 1950 году. Рекурсивное определение … Википедия
Многочлены Чебышева — Многочлены Чебышева две последовательности ортогональных многочленов и , названные в честь Пафнутия Львовича Чебышева. Многочлены Чебышева играют важную роль в теории приближений, поскольку корни многочленов Чебышева первого рода… … Википедия
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Многочлены Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмона Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Многочлены Лагерра также используются в… … Википедия
Многочлены Якоби — Полиномы Якоби класс ортогональных полиномов. Названы в честь Карла Густава Якоба Якоби. Ортогональные полиномы Якоби Открыты Якоби, Карл Густав Якоб Формула … Википедия
Многочлены Кравчука — ( М. Ф. Кравчук, 1929) относятся к классическим ортогональным полиномам дискретной переменной на равномерной сетке, для которых соотношение ортогональности представляет собой не интеграл, а ряд или конечную сумму: . Здесь весовая … Википедия
Ортогональные многочлены — Пафнутий Львович Чебышёв В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов … Википедия
Кравчук, Михаил Филиппович — Михаил Филиппович Кравчук укр. Михайло Пилипович Кравчук Д … Википедия
Кравчук, Михаил — Михаил Филиппович Кравчук (12 октября 1892[1], Човницы, ныне Волынская область 9 марта 1942, Колыма, лагерь ГУЛАГа) украинский математик. В 1910 году окончил гимназию в Луцке, с 1910 по 1914 учился на математическом отделении физико… … Википедия
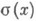есть ступенчатая функция со скачками 
