КОШИ ПРИЗНАК

КОШИ ПРИЗНАК

- 1) К. п. сходимости числового ряда: если для числового ряда с неотрицательными членами существует такое число что, начиная с нек-рого номера, выполняется неравенство равносильное условию то данный ряд сходится. Если же, начиная с нек-рого номера, имеет место неравенство или даже менее того существует подпоследовательность для членов к-рой имеет место неравенство 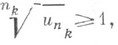то ряд расходится. В частности, если существует то ряд 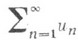сходится, если существует то ряд расходится. Установлен О. Коши [1]. Для рядов 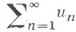с членами и п произвольных знаков из условия следует расходимость ряда; из условия

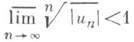- абсолютная сходимость ряда.

2) К. п. интегральный, интегральный признак Коши - Маклорена: если для числового ряда 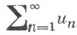с неотрицательными членами существует такая невозрастающая неотрицательная функция f(x), определенная при что то данный ряд сходится в том и только в том случае, когда сходится интеграл.

Впервые дан в геометрич. форме К. Маклореном [2], а впоследствии вновь открыт О. Коши [3]. Лит.: [1] Cauchy A. L., Analyse algebrique. P., 1821, p. 132-35; [2] М а с L a u r i n C., A treatise of fluxions, v. 1, Edinburgh, 1742, p. 289-90; [3] Cauchy A. L., CEuvres completes, ser. 2, t. 7, P., 1889, p. 268-79; [4] Никольский С. М., Курс математического анализа, 2 изд., т. 1, М., 1975. Л. Д. Кудрявцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "КОШИ ПРИЗНАК" в других словарях:

  • Признак — в математике, логике то же, что и достаточное условие. В менее строгих науках слово «признак» употребляется, как описание фактов, позволяющих (согласно существующей теории и т.п.) сделать вывод о наличии интересующего явления. Примеры… …   Википедия

  • Признак Ермакова — признак сходимости числовых рядов с положительными членами, установленный Василием Ермаковым. Его специфика заключается в том, что он превосходит все прочие признаки своей чувствительностью . Эта работа опубликована в статьях: «Общая теория… …   Википедия

  • Признак сходимости д’Аламбера — Признак д’Аламбера признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г. Если для числового ряда существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство …   Википедия

  • Признак сходимости Д’Аламбера — Признак Д’Аламбера признак сходимости числовых рядов, установлен Жаном Д’Аламбером в 1768 г. Если для числового ряда существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство то данный ряд абсолютно… …   Википедия

  • Признак сходимости Д'Аламбера — Признак Д’Аламбера признак сходимости числовых рядов, установлен Жаном Д’Аламбером в 1768 г. Если для числового ряда существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство то данный ряд абсолютно… …   Википедия

  • Признак Дирихле — Признак Дирихле  теорема, указывающая достаточные условия сходимости несобственных интегралов и суммируемости бесконечных рядов. Названа в честь немецкого математика Лежёна Дирихле. Содержание …   Википедия

  • Признак Лобачевского — признак сходимости числового ряда, предложенный Лобачевским между 1834 и 1836. Пусть есть убывающая последовательность положительных чисел, тогда ряд сходится или расходится одновременно с рядом …   Википедия

  • Признак Дини — Признак Дини  признак поточечной сходимости ряда Фурье. Несмотря на то, что ряд Фурье функции из сходится к ней в смысле нормы, он вовсе не обязан сходиться к ней поточечно (даже в случае непрерывной функции). Тем не менее, при некоторых… …   Википедия

  • Признак Жордана — признак сходимости рядов Фурье: если периодическая функция имеет ограниченную вариацию на отрезке , то её ряд Фурье сходится в каждой точке к числу ; если при этом функция непрерывна на отрезке …   Википедия

  • Признак Раабе — (признак Раабе Дюамеля) признак сходимости знакоположительных числовых рядов, установленный Йозефом Людвигом Раабе (Joseph Ludwig Raabe) и независимо Жан Мари Дюамелем. Содержание 1 Формулировка 2 Формул …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»