КОМПЛЕКСНЫЙ ТОР

- комплексная абелева группа Ли, получаемая из re-мерного комплексного пространства С ⁿ факторизацией по решетке ГМС ⁿ ранга 2п. К. т.- это единственные связные компактные комплексные группы Ли [1]. Каждое эрмитово скалярное произведение в С ⁿ определяет на Т=С ⁿ/Т кэлерову метрику, инвариантную относительно сдвигов. К. т. могут быть охарактеризованы также как единственные компактные кэлеровы параллелизуемые многообразия [2]. Группа автоморфизмов комплексного многообразия Тсовпадает с голоморфом группа Т как комплексной группы Ли.

Голоморфные р-формы на К. т. Тимеют вид

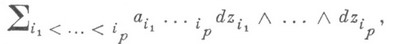
где 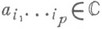, a z₁, . .., z_n- координаты в С ⁿ, и кольцо когомологий Дольбо естественно изоморфно (см. [1]).

Как вещественные группы Ли все n-мерные К. т. являются 2n-мерными торами и изоморфны между собой при фиксированном п. С точки зрения комплексной структуры положение гораздо сложнее. Базис решетки можно задать матрицей W. размера наз. матрицей периодов тора Т=С ⁿ/Г. Торы T_i=Cⁿ/Г _i с матрицами периодов W_i(i=1, 2) изоморфны между собой (как комплексные группы Ли или как комплексные многообразия) тогда и только тогда, когда существуют такие матрицы и ZGL(2n, Z), что W₂=CW₁Z.

Матрицу периодов любого n-мерного тора можно привести к виду ||EA||, где Im|A|>0. Торы с матрицами такого вида образуют голоморфное семейство, дающее эффективно параметризованную версальную деформацию любого n-мерного К. т., зависящую от п ² параметров [3]. В частности, при n=1 пространство параметров есть верхняя полуплоскость Im a>0 и множество классов изоморфных одномерных К. т. отождествляется с фактором {Im а>0}/D, где D - модулярная группа.

К. т., являющиеся алгебраич. многообразиями, наз. абелевими многообразиями. К. т. С ⁿ/Г - абелево многообразие тогда и только тогда, когда в С" существует эрмитово скалярное произведение, мнимая часть к-рого целочисленна на 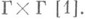В терминах матрицы периодов это условие выражается как условие Римана - Фробеннуса: должна существовать такая кососнмметрич. матрица что WQW' =0 и что 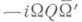положительно определена. При n=1 эти условия всегда выполнены; соответствующие алгебраич. кривые суть эллиптические кривые. Матрица периодов

дает пример двумерного К. т., не являющегося абелевым многообразием. На этом торе не существует даже непостоянных мероморфных функций [5]. Необходимым и достаточным условием алгебраичности n-мерного К. т. является также наличие на нем палгебраически независимых мероморфных функций.

Интерес к К. т. возник в 19 в. в связи с изучением абелевых функций, а также Якоби многообразий алгебраич. кривых. С любым n-мерным компактным кэлеровым многообразием Мсвязан набор n К. т.- его многообразий Якоби, к-рые являются абелевыми многообразиями, если Малгебраично [7].

Лит.:[1] Мамфорд Д., Абелевы многообразия, пер. с англ., М., 1971; [2] Wang Н. С, "Рrос. Amer. Math. Soc." 1954, v. 5, p. 771-76; [3] Коdairа К., Spenсer D. C, "Ann. Math.", 1958, v. 67, p. 328 - 466; [4] Вейль А., Введение в теорию кэлеровых многообразий, пер. с франц., М., 1961; [5] Зигель К. л., Автоморфные функции нескольких комплексных переменных, пер. с англ., М., 1954; [6] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [7] Чжень IIIэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961.

А. Л. Онищик.