КОНФОРМНО-ИНВАРИАНТНАЯ МЕТРИКА

КОНФОРМНО-ИНВАРИАНТНАЯ МЕТРИКА

на римановой поверхности R- правило, к-рое каждому локальному параметру z, отображающему параметрич. окрестность 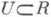в замкнутую комплексную плоскость 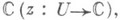ставит в соответствие действительную функцию

такую, что для всяких локальных параметров z1 : 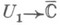и z2 : с непустым пересечением в последнем выполнено соотношение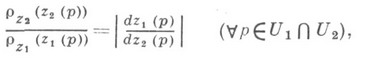

где z(U)- образ Uв при отображении z. К.-и. м. часто обозначается символом p(z)|dz|, к-рому приписывается указанная инвариантность относительно выбора локального параметра z.

Всякий линейный дифференциал k(z) dz или квадратичный дифференциал Q(z) dz2 порождает К.-и. м. соответственно |l(z)|-|dz| или 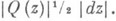Понятие

К.-и. м. позволяет ввести понятие длины для кривых на R, а также понятия экстремальной длины и модуля семейств кривых, являющиеся весьма общей формой определения конформных инвариантов (см. Экстремальной метрики метод, а также [1]). Определение К.-и. м. может быть перенесено на римановы многообразия любой размерности.

Лит.:[1] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962; [2] Шиффер М., Спенсер Д. К., Функционалы на конечных римановых поверхностях, пер. с англ., М., 1957; [3] Альфорс Л., Берс Л., Пространства римановых поверхностей и квазиконформные отображения, пер. с англ., М., 1961.

П. М. Тамразов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "КОНФОРМНО-ИНВАРИАНТНАЯ МЕТРИКА" в других словарях:

  • ГИПЕРБОЛИЧЕСКАЯ МЕТРИКА — гиперболическая мера, метрика в области комплексной плоскости, обладающей по крайней мере тремя граничными точками, инвариантная относительно автоморфизмов этой области. Гиперболическая метрика в круге Е : . определяется линейным элементом где… …   Математическая энциклопедия

  • ИНВАРИАНТНЫЙ ОБЪЕКТ — на однородном пространстве поле геометрич. величин на однородном пространстве M=G/H группы Ли G, не меняющееся при всех преобразованиях из G. Более строгое определение И. о. состоит в следующем. Пусть локально тривиальное однородное расслоение… …   Математическая энциклопедия

  • ГИПЕРБОЛИЧЕСКОЙ МЕТРИКИ ПРИНЦИП — пусть области Dи Gлежат соответственно в плоскостях и и имеют каждая не менее чем по три граничные точки, пусть функция, регулярная в Dи принимающая значения в G, и пусть и линейные элементы в гиперболич. метрике областей D и G в точках… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»