ИНДУЦИРОВАННОЕ РАССЛОЕНИЕ
- ИНДУЦИРОВАННОЕ РАССЛОЕНИЕ
- расслоение f* (p) : X' ->В', индуцированное отображением f : В'->В и расслоением p : где X'- подпространство прямого произведения
где X'- подпространство прямого произведения 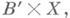 состоящее из пар (b', х), для которых f(b')=p(х), а f* (p) - отображение, определяемое соответствием
состоящее из пар (b', х), для которых f(b')=p(х), а f* (p) - отображение, определяемое соответствием 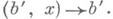 Отображение F:
Отображение F: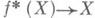 И. р. в исходное расслоение, определенное формулой F(b', х) = х, является морфизмом расслоений, накрывающим f. Для каждой точки
И. р. в исходное расслоение, определенное формулой F(b', х) = х, является морфизмом расслоений, накрывающим f. Для каждой точки 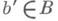 ограничения
ограничения
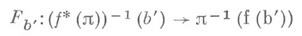
являются гомеоморфизмами. Кроме того, для любого расслоения h : и морфизма Н:
и морфизма Н: накрывающего f, существует один и только один В'-морфизм К:
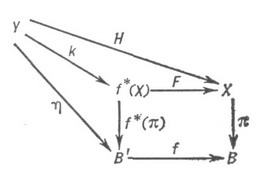
накрывающего f, существует один и только один В'-морфизм К: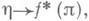 удовлетворяющий соотношениям FK=H,f*(p)K=h, так что имеет место коммутативная диаграмма:
удовлетворяющий соотношениям FK=H,f*(p)K=h, так что имеет место коммутативная диаграмма:
Расслоения, индуцированные изоморфными расслоениями, изоморфны, расслоение, индуцированное постоянным отображением, изоморфно тривиальному. Для любого сечения sрасслоения p отображение s: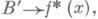 определенное формулой s(b')= (b',sf(b')), является сечением И. р. f* (л) и удовлетворяет соотношению Fs=sf. Напр., отображение я :
определенное формулой s(b')= (b',sf(b')), является сечением И. р. f* (л) и удовлетворяет соотношению Fs=sf. Напр., отображение я : индуцирует расслоение я 2 с пространством p*(х). и базой X- квадрат расслоения я, оно обладает единственным сечением s(x) = ( х, х).
индуцирует расслоение я 2 с пространством p*(х). и базой X- квадрат расслоения я, оно обладает единственным сечением s(x) = ( х, х).
Лит.:[1] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973; [2] Стинрод Н., Топология косых произведений, пер. с англ., М., 1953; [3] Xьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970.
М. И. Войцеховский.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ИНДУЦИРОВАННОЕ РАССЛОЕНИЕ" в других словарях:
Индуцированное расслоение — расслоение , индуцированное отображением и расслоением , где подпространство прямого произведения , состоящее из пар , для которых … Википедия
ГЛАВНОЕ РАССЛОЕНИЕ — расслоение такое, что группа Gдействует свободно и совершенно на пространстве X. Значение Г. р. состоит в том, что оно позволяет строить ассоциированные (с ним) расслоения со слоем F, если задано представление Gв группе гомеоморфизмов F.… … Математическая энциклопедия
ЛОКАЛЬНО ТРИВИАЛЬНОЕ РАССЛОЕНИЕ — расслоение со слоем F, для любой точки базы к рого существует окрестность и гомеоморфизм такой, что где Отображение наз. картой Л. т. р. Совокупность карт {hU}, ассоциированная с покрытием базы {U}, образует атлас Л. т. р. Напр., главное… … Математическая энциклопедия
Локально тривиальное расслоение — расслоение, которое локально выглядит как прямое произведение. Содержание 1 Определение 2 Связанные определения 3 Примеры … Википедия
ВЕКТОРНОЕ РАССЛОЕНИЕ — локально тривиальное расслоение : , каждый слои к рого наделен структурой (конечномерного) векторного пространства над телом ; наз. размерностью В. р. Сечения В. р. я образуют локально свободный модуль над кольцом непрерывных функций на Всо… … Математическая энциклопедия
Векторное расслоение — Векторным расслоением называется определённая геометрическая конструкция, соответствующая семейству векторных пространств, параметризованных другим пространством (например, может быть топологическим пространством, многообразием или алгебраической … Википедия
Нормальное расслоение — подмногообразия риманова многообразия векторное расслоение, состоящее из касательных векторов к объемлющему многообразию, которые перпендикулярны к Слой этого расслоения в точке называется нормальным пространством в точке Свойства Пусть … Википедия
КЛАССИФИЦИРУЮЩЕЕ ПРОСТРАНСТВО — база В 0 универсального расслоения x= (E0, р 0, В о). Универсальность расслоения x понимается в следующем смысле. Пусть kG (Х) множество классов эквивалентности (относительно изоморфизма, накрывающего тождественное отображение X)локально… … Математическая энциклопедия
Число Штифеля — Класс Штифеля Уитни определённый характеристический класс, соответствующий вещественному векторному расслоению . Обычно обозначается через w(E). Принимает значения в , кольце когомологий с коэффициентами в . Компонента w(E) в i ых когомологиях… … Википедия
Класс Штифеля — Уитни — Класс Штифеля Уитни определённый характеристический класс, соответствующий вещественному векторному расслоению . Обычно обозначается через w(E). Принимает значения в , кольце когомологий с коэффициентами в . Компонента w(E) в i ых… … Википедия
 где X'- подпространство прямого произведения
где X'- подпространство прямого произведения 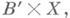 состоящее из пар (b', х), для которых f(b')=p(х), а f* (p) - отображение, определяемое соответствием
состоящее из пар (b', х), для которых f(b')=p(х), а f* (p) - отображение, определяемое соответствием 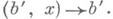 Отображение F:
Отображение F: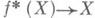 И. р. в исходное расслоение, определенное формулой F(b', х) = х, является морфизмом расслоений, накрывающим f. Для каждой точки
И. р. в исходное расслоение, определенное формулой F(b', х) = х, является морфизмом расслоений, накрывающим f. Для каждой точки 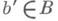 ограничения
ограничения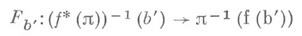
 и морфизма Н:
и морфизма Н: накрывающего f, существует один и только один В'-морфизм К:
накрывающего f, существует один и только один В'-морфизм К: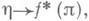 удовлетворяющий соотношениям FK=H,f*(p)K=h, так что имеет место коммутативная диаграмма:
удовлетворяющий соотношениям FK=H,f*(p)K=h, так что имеет место коммутативная диаграмма: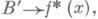 определенное формулой s(b')= (b',sf(b')), является сечением И. р. f* (л) и удовлетворяет соотношению Fs=sf. Напр., отображение я :
определенное формулой s(b')= (b',sf(b')), является сечением И. р. f* (л) и удовлетворяет соотношению Fs=sf. Напр., отображение я : индуцирует расслоение я 2 с пространством p*(х). и базой X- квадрат расслоения я, оно обладает единственным сечением s(x) = ( х, х).
индуцирует расслоение я 2 с пространством p*(х). и базой X- квадрат расслоения я, оно обладает единственным сечением s(x) = ( х, х).
