Число Штифеля

Класс Штифеля — Уитни — определённый характеристический класс, соответствующий вещественному векторному расслоению $E\rightarrow X$. Обычно обозначается через w(E). Принимает значения в $H^*(X;\;\Z_2)$, кольце когомологий с коэффициентами в $\Z_2=\Z/2\Z$.

Компонента w(E) в i-ых когомологиях $H^i(X;\;\Z_2)$ обозначается w_i(E) и называется i-ым классом Штифеля — Уитни расслоения E, так что

$w(E)=w_0(E)+w_1(E)+w_2(E)+\ldots\,.$

Классы w_i(E) являются препятствиями в $H^i(X;\;\Z_2)$ к построению (n − i + 1)-го линейно независимого сечения E, ограниченного на i-ый остов X.

Аксиоматическое определение

Здесь и далее, $H^i(X;\;G)$ обозначает сингулярные когомологии пространства X с коэффициентами в группе G.

Класс Штифеля — Уитни определяется как отображение, сопоставляющее расслоению E элемент кольца гомологий w(E) так, что выполняются следующие аксиомы:

1. Естественность: w(f ^* E) = f ^* w(E) для любого расслоения $E\to X$ и отображения $f:X'\to X$, где f ^* E обозначает соответствующее индуцированное расслоение над X'.
2. w₀(E) = 1 в $H^0(X;\;\Z/2\Z)$.
3. w₁(γ¹) является образующей $H^1(\R P^1;\;\Z/2\Z)\cong\Z/2\Z$ (условие нормализации). Здесь γ¹ — это тавтологическое расслоение.
4. $w(E\oplus F)= w(E)\smallsmile w(F)$ (формула произведения Уитни).

Можно показать, что удовлетворяющие этим аксиомам классы действительно существуют и единственны (по крайней мере, для паракомпактного пространства X)^[1]

Исходное построение

Классы Штифеля — Уитни w_i(E) были открыты Штифелем и Уитни как приведение по модулю 2 классов, измеряющих препятствия к построению (n − i + 1)-го линейно независимого сечения E, ограниченного на i-ый остов X. (Здесь n — размерность слоя F расслоения E).

Более точно, если X является CW-комплексом, Уитни определил классы W_i(E) в i-й группе клеточных когомологий X с нестандартными коэффициентами.

А именно, в качестве коэффициентов берётся (i − 1)-я гомотопическая группа многообразия Штифеля V_{n − i + 1}(F) наборов из n − i + 1 линейно независимого вектора в слое F. Уитни доказал, что для построенных им классов W_i(E) = 0 тогда и только тогда, когда расслоение E, ограниченное на i-скелет X, имеет n − i + 1 линейно независимое сечение.

Поскольку гомотопическая группа π_{i − 1}V_{n − i + 1}(F) многообразия Штифеля всегда или бесконечная циклическая, или изоморфна 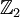$\Z_2$, существует каноническая редукция классов W_i(E) к классам $w_i(E)\in H^i(X;\;\Z_2)$, которые и называются классами Штифеля — Уитни.

В частности, если $\pi_{i-1}V_{n-i+1}(F)=\Z_2$, то эти классы просто совпадают.

Связанные определения

• Если мы работаем на многообразии размерности n, то любое произведение классов Штифеля — Уитни общей степени n может быть спарено с 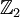$\Z_2$-фундаментальным классом этого многообразия, давая в результате элемент 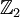$\Z_2$; такие числа называют числами Штифеля — Уитни векторного расслоения. К примеру, для расслоения на трёхмерном многообразии есть три линейно независимых числа Штифеля — Уитни, соответствующие $w_1^3$, w₁w₂ и w₃. В общем случае, если многообразие n-мерно, различные числа Штифеля — Уитни соответствуют разбиениям n в сумму целых слагаемых.
  • Числа Штифеля — Уитни касательного расслоения к гладкому многообразию называются числами Штифеля — Уитни этого многообразия. Они являются инвариантами кобордизма.
• Естественному отображению приведения по модулю два, $\Z\to\Z_2$, соответствует гомоморфизм Бокштейна

  $\beta\colon H^i(X;\;\Z_2)\to H^{i+1}(X;\;\Z).$

Образ класса w_i под его действием, $\beta w_i\in H^{i+1}(X;\;\Z)$, называется (i + 1)-ым целым классом Штифеля — Уитни.

• В частности, третий целый класс Штифеля — Уитни является препятствием к построению Spin^C-структуры.

Свойства

• Если расслоение E^k имеет $s_1,\;\ldots,\;s_\ell$ сечений, линейно независимых над каждой точкой, то $w_{k-\ell+1}=\ldots=w_k=0$.
• w_i(E) = 0 при i > rank(E).
• Первый класс Штифеля — Уитни обращается в ноль тогда и только тогда, когда расслоение ориентируемо. В частности, многообразие M ориентируемо тогда и только тогда, когда w₁(TM) = 0.
• Расслоение допускает спинорную структуру, тогда и только тогда, когда первый и второй классы Штифеля — Уитни оба обращаются в ноль.
• Для ориентируемого расслоения, второй класс Штифеля — Уитни лежит в образе естественного отображения $H^2(M,\;\Z)\to H^2(M,\;\Z_2)$ (или, что то же самое, так называемый третий целый класс Штифеля — Уитни обращается в ноль) тогда и только тогда, когда расслоение допускает Spin^C-структуру.
• Все числа Штифеля — Уитни гладкого компактного многообразия X обращаются в ноль тогда и только тогда, когда это многообразие является границей (без учёта ориентации) гладкого компактного многообразия.

Литература

• Прасолов В. В. Элементы теории гомологий.
• Husemoller D. Fibre Bundles. — Springer-Verlag, 1994.
• Милнор Дж., Сташев Дж. Характеристические классы. — М.: Мир, 1979. — 371 с.

Примечания

1. ↑ см. разделы 3.5 и 3.6 книги Хюсмоллера или раздел 8 в Милноре — Сташеве.