- ИЗМЕРИМАЯ ФУНКЦИЯ
- 1) В первоначальном понимании И. ф.- функция f(x)действительного переменного, обладающая тем свойством, что для любого амножество Е а точек х, для к-рых f(x)<a есть измеримое множество (по Лебегу). И. ф. на отрезке [ х 1, х 2]может быть сделана непрерывной на [x1, x2]путем изменения ее значений на множестве сколь угодно малой меры; это - так наз. С-свойство И. ф. (Н. Н. Лузин, 1913).
2) И. ф. на пространстве Xопределяется относительно выбранной системы измеримых множеств Ав X. Если A есть s-кольцо, то действительная функция f, заданная на пространстве X, наз. измеримой функцией, если

для любого действительного а, где

Это определение равносильно следующему: действительная j функция f измерима, если
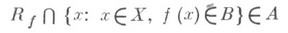 для любого борелевского В. В случае, когда Аесть s-алгебра, функция f является измеримой, если измеримы множества Е а (или
для любого борелевского В. В случае, когда Аесть s-алгебра, функция f является измеримой, если измеримы множества Е а (или 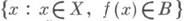 ). Класс И. ф. замкнут относительно арифметических и структурных операций, т. е., если fn, n=1, 2, ... измеримы, то f1+f2, f1f1. max(f1, f2), min(f1, f2), af, где адействительно, измеримы;
). Класс И. ф. замкнут относительно арифметических и структурных операций, т. е., если fn, n=1, 2, ... измеримы, то f1+f2, f1f1. max(f1, f2), min(f1, f2), af, где адействительно, измеримы; 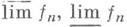 тоже измеримы. Комплексная функция измерима, если измеримы ее действительная и мнимая части. Обобщением понятия И. ф. является понятие измеримого отображения одного измеримого пространства в другое.
тоже измеримы. Комплексная функция измерима, если измеримы ее действительная и мнимая части. Обобщением понятия И. ф. является понятие измеримого отображения одного измеримого пространства в другое.Лит.:[1] Xалмош П., Теория меры, пер. с англ.,М. 1953; [2] Данфорд Н., Шварц Д ж. Т., Линейные операторы, пер. с англ., т. 1, М., 1962; [3] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976.
В. В. Сазонов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
