- ЭКСЦЕССИВНАЯ ФУНКЦИЯ
для марковского процесса - аналог неотрицательной супергармонической функции.
Пусть в измеримом пространстве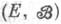 задана однородная марковская цепь с вероятностями перехода за один шаг
задана однородная марковская цепь с вероятностями перехода за один шаг  Измеримая относительно
Измеримая относительно 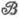 функция
функция  наз. эксцессивной функцией для этой цепи, если
наз. эксцессивной функцией для этой цепи, если 
всюду в Е. Для цепи с не более чем счетным множеством состояний среди Э. ф. есть отличные от констант тогда и только тогда, когда хоть одно из состояний невозвратно.
При заданном в однородном марковском процессе
однородном марковском процессе  с переходной функцией P(t,x, В )определение Э. <ф. несколько усложнится. Множество Вотносят к
с переходной функцией P(t,x, В )определение Э. <ф. несколько усложнится. Множество Вотносят к  -алгебре
-алгебре  если для любой конечной меры
если для любой конечной меры  на
на  найдутся такие множества
найдутся такие множества  и
и  что
что 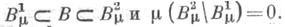 Функция
Функция 
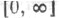 наз. эксцессивной функцией, если она
наз. эксцессивной функцией, если она  -измерима и при
-измерима и при  удовлетворяет всюду в Есоотношениям
удовлетворяет всюду в Есоотношениям 
и
Для части винеровского процесса в нек-рой области
 (см. Функционал от марковского процесса) совпадает с классом неотрицательных супергармонических в Ефункций, пополненным функцией
(см. Функционал от марковского процесса) совпадает с классом неотрицательных супергармонических в Ефункций, пополненным функцией 
В случае стандартного процесса Xв локально компактном сепарабельном пространстве Е, для Э. ф. f(х) всюду в Евыполняется неравенство где
где  -марковский момент, М х - математическое ожидание, отвечающее мере Р х, и где положено
-марковский момент, М х - математическое ожидание, отвечающее мере Р х, и где положено 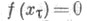 при
при  Другое часто используемое свойство Э. ф. состоит в том, что Р х - почти наверное случайная функция f (х t) непрерывна справа на интервале
Другое часто используемое свойство Э. ф. состоит в том, что Р х - почти наверное случайная функция f (х t) непрерывна справа на интервале 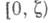 (см. [3]).
(см. [3]).
Э. ф. наз. гармонической, если, как бы ни задавался компакт
наз. гармонической, если, как бы ни задавался компакт 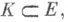 выполняется
выполняется 
 где
где  -момент первого выхода Xиз К. Потенциалом наз. любую Э. ф.
-момент первого выхода Xиз К. Потенциалом наз. любую Э. ф.  для к-рой
для к-рой 
при любом выборе марковских моментов таких, что
таких, что  при
при 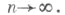 Для части винеровского процесса в области
Для части винеровского процесса в области 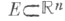 гармонич. функции и потенциалы, это, соответственно, неотрицательные в Егармонические в классич. смысле функции и потенциалы Грина борелевских мер, сосредоточенных в Е.
гармонич. функции и потенциалы, это, соответственно, неотрицательные в Егармонические в классич. смысле функции и потенциалы Грина борелевских мер, сосредоточенных в Е.
Примером потенциала служит потенциал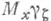 аддитивного функционала
аддитивного функционала 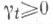 от X, если
от X, если  Э. ф.
Э. ф.  является потенциалом аддитивного функционала в том и только том случае, когда
является потенциалом аддитивного функционала в том и только том случае, когда 
где
 - момент 1-го попадания в множество
- момент 1-го попадания в множество 

В рамках аксиоматич. теории гармонич. пространств Брело все неотрицательные супергармонич. функции являются Э. ф. для нек-рого стандартного процесса.
См. также Мартина граница, Ляпунова стохастическая функция.Лит.:[1] Хант Дж.-А., Марковские процессы и потенциалы, пер. с англ., М., 1962; [2] Ширяев А. Н., Статистический последовательный анализ, 2 изд., М., 1976: [3] Дынкин Е. Б., Марковские процессы, М., 1963; [4] Getoor R. К., Markov processes: Ray processes and right prosesses, В., 1975; [5] Шур М. Г., лМатем. заметки
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
