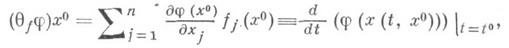ДИФФЕРЕНЦИРОВАНИЕ В СИЛУ СИСТЕМЫ
- ДИФФЕРЕНЦИРОВАНИЕ В СИЛУ СИСТЕМЫ
- оператор, к-рый определяется следующим образом. Пусть

-автономная система, f=(f1, ... ,fn) и fj : G
f=(f1, ... ,fn) и fj : G R - гладкие отображения, где G- область в Rn. Пусть дано гладкое отображение j :
R - гладкие отображения, где G- область в Rn. Пусть дано гладкое отображение j :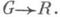 Производная qfj в силу системы (*) функции j в точке
Производная qfj в силу системы (*) функции j в точке 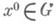 определяется выражением
определяется выражением
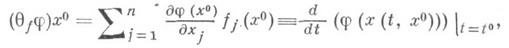
где x(t, х 0)- решение системы (*) такое) что x(t0, х 0)=х 0. Свойства оператора qf:1) линейность по j, 2) qf(j1j2)=j1qfj2+j2qfj1. Функция (qfj)(x)совпадает с производной j по векторному полю f.
Лит.:[1] Понтрягин Л. С, Обыкновенные дифференциальные уравнения, 3 изд., М., 1970.
М. В. Федорюк
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ДИФФЕРЕНЦИРОВАНИЕ В СИЛУ СИСТЕМЫ" в других словарях:
Приближенное дифференцирование — Постановка задачи приближенного дифференцирования. При решении практических задач часто нужно найти производные указанных порядков от функции y = f(x), заданной таблично, кроме того, возможно также, что в силу сложности аналитического выражения… … Википедия
НЕЛИНЕЙНЫЕ СИСТЕМЫ — колебательные системы, св ва к рых зависят от происходящих в них процессов. Колебания таких систем описываются нелинейными ур ниями. Нелинейными явл.: механич. системы, где модули упругости тел зависят от деформаций последних или коэфф. трения… … Физическая энциклопедия
ДУГА БЕЗ КОНТАКТА — гладкая кривая без самопересечений на фазовой плоскости двумерной автономной системы дифференциальных уравнений обладающая тем свойством, что в каждой точке этой кривой вектор фазовой скорости системы (см. Фазовой скорости вектор). определен,… … Математическая энциклопедия
ЧЕТАЕВА ФУНКЦИЯ — функция v(x) и окрестности неподвижной точки х =0 системы обыкновенных дифференциальных уравнений обладающая двумя свойствами: 1) существует примыкающая к точке x=0 область G, в к рой v>0, и v=0 на границе области Gвблизи x=0; 2) в области… … Математическая энциклопедия
Мышцы* — мускулы (Musculi состоящие из особой ткани [мускульной, или мышечной] см. ниже) органы животных, которые, обладая в высшей степени способностью сокращаться в определенном направлении, служат главными активными органами движения животных… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Мышцы — мускулы (Musculi состоящие из особой ткани [мускульной, или мышечной] см. ниже) органы животных, которые, обладая в высшей степени способностью сокращаться в определенном направлении, служат главными активными органами движения животных… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Евро — (Euro) Евро это единая европейская валюта Евро: описание монет и банкнот, история создания и развития, место в мировой экономике Содержание >>>>>>>>>> … Энциклопедия инвестора
Спенсер Герберт — (Spencer) один из величайших английских мыслителей. С. родился в 1820 г. (27 апреля) в Дерби. Его отец был учителем. Влияние его на сына было благотворно в том отношении, что он с ранних лет пробуждал в ребенке самодеятельность и независимость… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Спенсер, Герберт — I (Spencer) один из величайших английских мыслителей. С. родился в 1820 г. (27 апреля) в Дерби. Его отец был учителем. Влияние его на сына было благотворно в том отношении, что он с ранних лет пробуждал в ребенке самодеятельность и независимость… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
СУПЕРСИММEТРИЯ — симметрия физ. системы, объединяющая состояния, подчиняющиеся разным статистикам статистике Бозе Эйнштейна (бозоны) и статистике Ферми Дирака (фермионы). Принципиальные основы С. сформулированы в нач. 1970 х гг. в работах [1, 2, 3]. В последующие … Физическая энциклопедия

 f=(f1, ... ,fn) и fj : G
f=(f1, ... ,fn) и fj : G R - гладкие отображения, где G- область в Rn. Пусть дано гладкое отображение j :
R - гладкие отображения, где G- область в Rn. Пусть дано гладкое отображение j :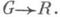 Производная qfj в силу системы (*) функции j в точке
Производная qfj в силу системы (*) функции j в точке 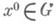 определяется выражением
определяется выражением