Приближенное дифференцирование

Приближенное дифференцирование

Постановка задачи приближенного дифференцирования.

При решении практических задач часто нужно найти производные указанных порядков от функции y = f(x), заданной таблично, кроме того, возможно также, что в силу сложности аналитического выражения функции f(x) непосредственное дифференцирование ее затруднительно. В этих случаях обычно прибегают к приближенному дифференцированию.

Файл:Http://pixs.ru/showimage/NewBitmapI 9755888 404126.jpg

Для вывода формул приближенного дифференцирования заменяют данную функцию f(x) на интересующем отрезке [a,b] интерполирующей функцией P(x) (чаще всего полиномом), а затем полагают:

$\frac{df(x)}{dx} = P'(x)$, при:

$a \le \ x \le \ b$.

Аналогично поступают при нахождении производных высших порядков функции f(x).

Если для интерполирующей функции P(x) известна погрешность: $\ R(x) = f(x) - P(x)$,

то погрешность производной P'(x) выражается формулой: $r(x) = \frac{df(x)}{dx} - P'(x) = R'(x)$

т. е. погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же самое справедливо и для производных высших порядков.

Следует отметить, что, вообще говоря, приближенное дифференцирование представляет собой операцию менее точную, чем интерполирование. Действительно, близость друг к другу ординат двух кривых

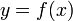$\ y = f(x)$ и $\ Y = P(x)$

на отрезке [a,b] еще не гарантирует близости на этом отрезке их производных $\frac{df(x)}{dx}$ и $\frac{dP(x)}{dx}$, т. е. малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.

Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона

Пусть имеем функцию $\ y(x)$, заданную в равноотстоящих точках $\ x_i (i=0, 1,2 ... n)$ отрезка $\ [a,b]$ с помощью значений $\ y_i = f(x_i)$.

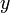Для нахождения на $\ [a,b]$ производных $\ y' = f'(x)$, $\ y' = f'(x)$ и т. д.^[1] функцию $\ y$ приближенно заменим интерполяционным полиномом Ньютона, построенным для системы узлов $\ x_0, x_1, ... x_k (k \le n)$.

Имеем:

$\ y(x) = y_0 \ + \ q\Delta y_0 \ + \ \frac{q(q-1)}{2!}\Delta^2 y_0 \ + \ \frac{q(q-1)(q-2)}{3!}\Delta^3 y_0 \ + \ \frac{q(q-1)(q-2)(q-3)}{4!}\Delta^4 y_0 \ + \ ..., \quad (1)$

где $\ q = \frac{x - x_0}{h}$ и $\ h = x_{i+1} - x_i \quad (i = 0,1, ...)$.

Производя перемножение биномов, получим:

$\ y(x) = y_0 \ + \ q\Delta y_0 \ + \ \frac{q^2-q}{2}\Delta^2 y_0 \ + \ \frac{q^3-3q^2+2q}{6}\Delta^3 y_0 \ + \ \frac{q^4-6q^3+11q^2-6q}{24}\Delta^4 y_0 \ + \ ..., \quad (1')$

Так как $\frac{dy}{dx} \ = \ \frac{dy}{dq} \cdot \frac{dq}{dx}$ ^[2]$= \frac{dy}{dx} \ = \ \frac{1}{h}\frac{dy}{dq}$

то

$\ y'(x) = \ \frac{1}{h} \Bigg[ y_0 \ + \ \frac{2q - 1}{2}\Delta^2 y_0 \ + \ \frac{3q^2-6q+2}{6}\Delta^3 y_0 \ + \ \frac{2q^3-9q^2+11q-3}{12}\Delta^4 y_0 \ + \ ... \Bigg]. \quad (2)$

Аналогично, так как $y''(x) \ = \ \frac{d(y')}{dx} \ = \ \frac{d(y')}{dq} \cdot \frac{dq}{dx} \ ,$

то

$\ y''(x) = \ \frac{1}{h^2} \Bigg[ \Delta^2 y_0 \ + \ (q - 1)\Delta^3 y_0 \ + \ \frac{6q^2-18q+11}{12}\Delta^4 y_0 \ + \ ... \Bigg]. \quad (3)$

Таким же способом можно вычислить производные функции $\ y(x)$ любого порядка

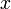При нахождении производных $\ y',y'', \ ...$ в фиксированной точке $\ x$ в качестве 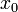$\ x_0$ выбирают ближайшие табличные значения аргумента.

В том случае, если необходимо найти производные функции 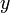$\ y$ в основных табличных точках $\ x_i$, то полагают $\ x = x_0$, следовательно $\ q = 0$ и получают:

$\ y'(x) = \ \frac{1}{h} \Bigg[ y_0 \ - \ \frac{ \Delta^2 y_0}{2} \ + \ \frac{\Delta^3 y_0}{3} \ - \ \frac{ \Delta^4 y_0}{4} \ + \ \frac{\Delta^5 y_0}{5} \ - \ ... \Bigg]. \quad (4)$

$\ y''(x) = \ \frac{1}{h^2} \Bigg[ \Delta^2 y_0 \ - \ \Delta^3 y_0 \ + \ \frac{11}{12}\Delta^4 y_0 \ + \ \frac{5}{6}\Delta^5 y_0 \ + \ ... \Bigg]. \quad (5)$

Формулы $\ (2)-(5)$ применяют, для начальных строк таблицы. Для последних строк таблицы используют формулы получающиеся при дифференцировании второй интерполяционной формулы Ньютона

Если $\ P_k(x)$ - интерполяционный полином Ньютона, содержащий разности $\ \Delta y_0, \Delta^2 y_0, \ ..., \ \Delta^k y_0$ и

$\ R_k'(x) = y'(x) - P_k'(x)$

Известно что:

$\ R_k(x) = \frac{(x-x_0)(x-x_1)...(x-x_k)}{(k+1)!}y^{(k+1)}(\xi) = h^{k+1} \frac{(q-1)...(q-k)}{(k+1)!}y^{(k+1)}(\xi)$

где ξ - некоторое промежуточное значение между узлами интерполирования $\ \ x_0, x_1, \ ..., \ x_k \$и рассматриваемой точной $\ \ x$. Поэтому, полагая, что $\ y(x) \in C^{(k+2)}$, получим:

$\ R_k'(x) = \frac{dR_k}{dq} \cdot \frac{dq}{dx} = \frac{h^k}{(k+1)!}\Bigg\{ y^{(k+1)}(\xi)\frac{d}{dq}\big[q(q-1) \ ... \ (q-k)\big] \ + \ q(q-1)...(q-k)\frac{d}{dq}\big[ y{(k+1)}(\xi)\big] \Bigg\}$

Отсюда при $\ \ x = x_0$ и, следовательно, при $\ \ q = 0$ и учитывая, что $\ \frac{d}{dq}\big[q(q-1) \ ... \ (q-k)\big]_{q=0} = (-1)^kk!$? ,будем иметь:

$\ R_k'(x_0) = (-1)^k \frac{h^k}{k+1}y^{(k+1)}(\xi)$.

Так как $\ y^{(k+1)}(\xi) \ .$ во многих случаях трудно оценить, то при <\math>\ h</math> малом приближенно полагают:

$\ y^{(k+1)}(\xi) \ \approx \ \frac{\Delta^{k+1}y_0}{h^{k+1}}$

и, следовательно,

$\ R_k'(x_0) \ \approx \ \frac{(-1)^k}{h}\frac{\Delta^{k+1}y_0}{k+1}$.

Аналогично может быть найдена погрешность $\ \ R_k''(x_0)$ для второй производной $\ \ y''(x_0)$

1. ↑ ¹ Cамо собой разумеется, что заранее должно быть известно о существовании соответствующих производных функции.

2. ↑ ² Производная сложной функции

Примеры нахождения производных по первой интерполяционной формуле Ньютона

Пример 1.Найти $\ y'(50)$ функции $\ y = ln(x)$, заданной таблично

x	y	Δy	Δ2y	Δ3y
$\ 50$	$\ 1,6990$	$\ 0,0414$	$\ -0,0036$	$\ 0,0005$
$\ 55$	$\ 1,7404$	$\ 0,0378$	$\ -0,0031$
$\ 60$	$\ 1,7782$	$\ 0,0347$
$\ 65$	$\ 1,8129$

Решение. Здесь h = 5. Дополняем таблицу столбцами конечных разностей. Используя первую строчку таблицы, на основании формулы (4) с точностью до разностей третьего порядка, будим иметь:

$\ y'(50)=\frac{1}{5}\big(0,0414+0,0018+0,0002\big)=0,0087$.

Для оценки точности найденного значения заметим, что так как табулированная выше функция есть $\ \ y = ln(x)$, то

$\ y'_x =\frac{M}{x}=\frac{0,43429}{x}$.

Следовательно,

$\ y'(50) = \frac{0,43429}{50}=0,0087$.

Таким образом результаты совпадают с точностью до четвертого десятичного знака.

Пример 2. Путь y = f(t), пройденный прямолинейно движущейся точкой за время t, дается в следующей таблице:

$\ l$	Время $\ t_i$ в сек.	Путь $\ y(t_i)$ в см
$\ 0$	$\ 0,00$	$\ 0,000$
$\ 1$	$\ 0,01$	$\ 1,519$
$\ 2$	$\ 0,02$	$\ 6,031$
$\ 3$	$\ 0,03$	$\ 13,397$
$\ 4$	$\ 0,04$	$\ 23,396$
$\ 5$	$\ 0,05$	$\ 35,721$
$\ 6$	$\ 0,06$	$\ 50,000$
$\ 7$	$\ 0,07$	$\ 65,798$
$\ 8$	$\ 0,08$	$\ 82,635$
$\ 9$	$\ 0,09$	$\ 100,000$

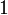
Используя конечные разности до пятого порядка включительно, приближенно найти скорость $\ V = \frac{dy}{dt}$ и ускорение $W = \frac{d^2y}{dt^2}$ точки для моментов $\ t = 0;0,001;0,02;0,03;0,04$

Решение. Составим таблицу разностей:

$\ l$	$\ \Delta y_i$	$\ \Delta^2 y_i$	$\ \Delta^3 y_i$	$\ \Delta^4 y_i$	$\ \Delta^5 y_i$
$\ 0$	$\ 1,519$	$\ 2,993$	$\ -0,139$	$\ -0,082$	$\ -0,004$
$\ 1$	$\ 4,512$	$\ 2,854$	$\ -0,221$	$\ -0,086$	$\ 0,021$
$\ 2$	$\ 7,366$	$\ 2,633$	$\ -0,307$	$\ -0,065$	$\ 0,002$
$\ 3$	$\ 9,999$	$\ 2,326$	$\ -0,372$	$\ -0,063$	$\ 0,018$
$\ 4$	$\ 12,325$	$\ 1,954$	$\ -0,435$	$\ -0,045$	$\ 0,014$
$\ 5$	$\ 14,279$	$\ 1,519$	$\ -0,480$	$\ -0,031$
$\ 6$	$\ 15,798$	$\ 1,039$	$\ -0,511$
$\ 7$	$\ 16,837$	$\ 0,528$
$\ 8$	$\ 17,365$
$\ 9$

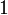
Полагая что $\ h = 0,$ и применяя формулы $\ (4)$ и $\ (5)$, получаем приближенные значения велечины скорости $\ V$ $\ \bigg(\frac{cm}{c}\bigg)$ и велечины ускорения $\ W$ $\ \bigg( \frac{cm}{c^2} \bigg)$. Например,

$\ V(0) = 100\big(1,519-1,496-0,046+0,020-0,001\big) = -0,4 \ \bigg(\frac{cm}{c} \bigg)$.

$\ W(0) = 100000\big(2,993+0,139-0,075+0,003\big) = 30600 \ \bigg(\frac{cm}{c^2} \bigg)$.

Cоответствующие значения $\ V$ и $\ W$ помещены в следующией таблице:

$\ t$	$\ V$	$\ W$	$\ \bar V$	$\ \bar W$
$\ 0,00$	$\ 0,4$	$\ 30600$	$\ 0,00$	$\ 30462$
$\ 0,01$	$\ 303,6$	$\ 29780$	$\ 303,08$	$\ 30001$
$\ 0,02$	$\ 596,3$	$\ 28780$	$\ 596,98$	$\ 28625$
$\ 0,03$	$\ 873,2$	$\ 26250$	$\ 872,66$	$\ 26381$
$\ 0,04$	$\ 1121,7$	$\ 23360$	$\ 1121,9$	$\ 23340$

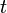
Заметим, что табулированны закон движения дается формулой

$\ y = 100 \bigg( 1-\cos\frac{50\pi t}{9}\bigg)$

Отсюда

$\ V= \frac{dy}{dt} = \frac{5000\pi}{9} \sin \frac{50\pi t}{9}$

и

$\ W= \frac{d^2y}{dt^2} = \frac{25000\pi}{81} \cos \frac{50\pi t}{9}$

Для сравнения точные значения $\ \bar V$ и $\ \bar W$ приведены в правой половине таблицы.

Связать^?