ДАРБУ УРАВНЕНИЕ

ДАРБУ УРАВНЕНИЕ

- 1) Д. у.- обыкновенное дифференциальное уравнение

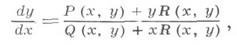
где Р, Q, R- целые многочлены относительно хи у. Это уравнение впервые исследовал Г. Дарбу [1]. Частный случай Д. у.- Якоби уравнение. Пусть п- высшая степень многочленов Р, Q, R;если Д. у. имеет s известных частных алгебраических решений, то при его общее решение отыскивается без квадратур, а при можно найти интегрирующий множитель (см. [2]). Если Ри Q - однородные функции степени то, a R- однородная функция степени к, то при к=т-1 Д. у. является однородным дифференциальным уравнением, а при подстановкой y=zx Д. у. приводится К Бернулли уравнению.

Лит.:[1] Darboux G., "Bull. sci. math.", 1878, t. 2, p. 66-96; [2] Айнс Э. Л. Обыкновенные дифференциальные уравнения, пер. с англ., Хар., 1939.

Н. <Х. <Розов.

2) Д. у.- гиперболическое уравнение

где X(t, x)- неотрицательная, непрерывно дифференцируемая функция, х=( х 1, х 2,. . ., х п). Для решений Д. у., как и для решений волнового уравнения, справедлива следующая теорема единственности. Если какое-нибудь дважды непрерывно дифференцируемое решение и( х, t )Д. у. обращается вместе со своей производной по tв нуль на основании, лежащем в плоскости t=0, характеристич. конуса, то оно равно нулю внутри всей области, ограниченной этим конусом. Характеристич. конус имеет тот же вид, что и для волнового уравнения.

При l(t, х) = п-1 > 0 решением Д. у., удовлетворяющим начальным условиям

с дважды непрерывно дифференцируемой функцией j(х), является функция

где Г(z) - гамма-функция. Это решение Д. у. и решение v(x, t )волнового уравнения, удовлетворяющее условиям

связаны соотношением

Д. у. названо по имени Г. Дарбу (G. Darboux).

Лит.:[1] Ион Ф., Плоские волны и сферические средние в применении к дифференциальным уравнениям с частными производными, пер. с англ., М., 1958.

А. К. Гущин.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем написать курсовую

Полезное


Смотреть что такое "ДАРБУ УРАВНЕНИЕ" в других словарях:

  • КЭЛИ - ДАРБУ УРАВНЕНИЕ — дифференциальное уравнение с частными производными третьего порядка, к рому должна удовлетворять функция u(x1, х 2, х 3).для того, чтобы семейство поверхностей u(x1, х 2, х 3) = const могло быть дополнено до трижды ортогональной системы… …   Математическая энциклопедия

  • Дарбу, Жан Гастон — Жан Гастон Дарбу фр. Jean Gaston Darboux …   Википедия

  • Уравнение Кэли — Дарбу  дифференциальное уравнение с частными производными третьего порядка, которому должна удовлетворять функция для того, чтобы семейство поверхностей могло быть дополнено до трижды ортогональной системы поверхностей. Уравнение Кэли Дарбу… …   Википедия

  • ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида где F заданная действительная функция точки х=(xt, ..., х п )области Dевклидова пространства Е п, и действительных переменных (и(х) неизвестная функция) с неотрицательными целочисленными индексами i1 ,..., in, k=0, ..., т, по… …   Математическая энциклопедия

  • ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА — уравнение, к рое содержит хотя бы одну производную 2 го порядка от неизвестной функции и(х)и не содержит производных более высокого порядка. Напр., линейное уравнение 2 го порядка имеет вид где точка х ( х 1, х 2, ..., х п )принадлежит нек рой… …   Математическая энциклопедия

  • МОНЖА - АМПЕРА УРАВНЕНИЕ — дифференциальное уравнение с частными производными 2 го порядка вида коэффициенты к рого зависят от переменных x, у, неизвестной функции z( х, у )и ее первых производных Тип М. А. у. зависит от знака выражения Если , М. А. у. есть уравнение… …   Математическая энциклопедия

  • Функциональное уравнение Коши — для функции имеет вид . Функцию, удовлетворяющую этому уравнению, называют аддитивной. Этот термин применяется для произвольных функций, не только над . Уравнение Коши является одним из старейших и наиболее простых функциональных уравнений,… …   Википедия

  • ЯКОБИ УРАВНЕНИЕ — обыкновенное дифференциальное уравнение 1 го порядка или, в более симметричной форме, где все коэффициенты постоянные числа. Это уравнение, являющееся частным случаем Дарбу уравнения, впервые исследовал К. Якоби [1]. Я. у. всегда интегрируется в… …   Математическая энциклопедия

  • СМЕШАННАЯ И КРАЕВАЯ ЗАДАЧИ ДЛЯ ГИПЕРБОЛИЧЕСКИХ УРАВНЕНИЙ И СИСТЕМ — задачи отыскания решений уравнений и систем с частными производными гиперболич. типа, удовлетворяющих на границе области их задания (или ее части) определенным условиям (см. Краевые условия, Начальные условия). Краевая задача для гиперболич.… …   Математическая энциклопедия

  • Ортогональные многочлены — Пафнутий Львович Чебышёв В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»