- ГРУППОВАЯ АЛГЕБРА
локально бикомпактной группы - топологическая алгебра с инволюцией, образованная функциями на группе и такая, что в ней умножение определяется как свертка. Пусть банахово пространство
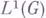 построено с помощью левоинвариантной Хаара меры
построено с помощью левоинвариантной Хаара меры . на локально бикомпактной топологич. группе G н пусть в
. на локально бикомпактной топологич. группе G н пусть в  умножение определяется как свертка
умножение определяется как свертка 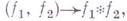 а инволюция
а инволюция  - по формуле
- по формуле 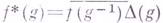 , где
, где  - модуль группы G. Полученная банахова алгебра с инволюцией наз. групповой алгеброй группы G и обозначается также через
- модуль группы G. Полученная банахова алгебра с инволюцией наз. групповой алгеброй группы G и обозначается также через 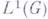 . Если G - конечная группа, то определение Г. а. совпадает с обычным алгебраич. определением Г. а. над полем комплексных чисел.
. Если G - конечная группа, то определение Г. а. совпадает с обычным алгебраич. определением Г. а. над полем комплексных чисел.
Понятие Г. а. позволяет применять общие методы теории банаховых алгебр в задачах теории групп и, в частности, в абстрактном гармонич. анализе. Свойства Г. а. как банаховой алгебры отражают свойства топологич. группы: так, Г. а. содержит единичный элемент тогда и только тогда, когда группа дискретна; Г. а. является прямой суммой (топологической) своих конечномерных минимальных двусторонних идеалов тогда н только тогда, когда группа бикомпактна. Исключительно важную роль играет понятие Г. а. в теории унитарных представлений группы: между непрерывными унитарными представлениями топологич. группы G и невырожденными симметричными представлениями Г. а.
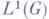 существует взаимно однозначное соответствие, сопоставляющее непрерывному унитарному представлению p группы G в гильбертовом пространстве Нпредставление Г. а.
существует взаимно однозначное соответствие, сопоставляющее непрерывному унитарному представлению p группы G в гильбертовом пространстве Нпредставление Г. а.  , определяемое формулой
, определяемое формулой
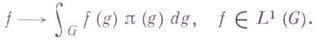
Г. а. локально бикомпактных групп обладают рядом общих свойств. Именно, любая Г. а. содержит аппроксимативную единицу (см. Банахова алгебра), образованную семейством характеристпч. функций окрестностей единичного элемента, упорядоченных по включению (ь сторону убывания); поэтому для Г. а. можно установить соответствие между положительными функционалами на Г. а. н ее симметричными представлениями. Любая Г. а. является полупростой алгеброй и имеет симметричное точное представление. В частности, представление Г. а., определяемое регулярным представлением группы, является точным. Замкнутые левые идеалы
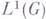 суть замкнутые векторные подпространства
суть замкнутые векторные подпространства  , инвариантные относительно левого сдвига.
, инвариантные относительно левого сдвига.
Иногда групповой алгеброй наз. банахова алгебра с инволюцией, полученная из Г. а.
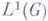 присоединением единицы. Существует ряд других алгебр с инволюцией, к-рые иногда наз. групповыми алгебрами. К их числу относятся, в частности: алгебра мер
присоединением единицы. Существует ряд других алгебр с инволюцией, к-рые иногда наз. групповыми алгебрами. К их числу относятся, в частности: алгебра мер 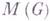 относительно свертки; алгебры относительно обычного умножения, напр, алгебра
относительно свертки; алгебры относительно обычного умножения, напр, алгебра 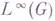 существенно ограниченных измеримых по мере Хаара функций, алгебра
существенно ограниченных измеримых по мере Хаара функций, алгебра  комплексных линейных комбинаций непрерывных положительно определенных функций. Множество
комплексных линейных комбинаций непрерывных положительно определенных функций. Множество 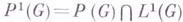 и совокупность
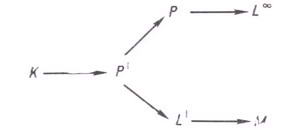
и совокупность 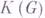 непрерывных финитных функций образуют алгебру и относительно свертки, и относительно обычного умножения. Имеет место следующая таблица, в к-рой стрелки означают включения:
непрерывных финитных функций образуют алгебру и относительно свертки, и относительно обычного умножения. Имеет место следующая таблица, в к-рой стрелки означают включения:
Лит.:[1] Наймарк М. А., Нормированное кольца 2 изд., М.. 1968; [2] Guichardet A., Analyse harmonique commutative, P., 1968. А. И. Штерн.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
