ФРОБЕНИУСОВА АЛГЕБРА

- конечномерная алгебра Rнад полем Ртакая, что левые R-модули . и Ноm _р (R, Р)изоморфны. На языке представлении это означает эквивалентность правого и левого регулярных представлений. Всякая групповая алгебра конечной группы над полем является Ф. а. Каждая Ф. а. является квазифробениусовым кольцом. Обратное утверждение неверно. Эквивалентны следующие свойства конечномерной Р-алгебры R:
1) R - Ф. а.;
2) существует такая невырожденная билинейная форма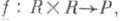 что f(ab, c)=f(a, bс )для любых а, b,
3) если L - левый, а Н- правый идеалы алгебры R, то (см. Аннулятор)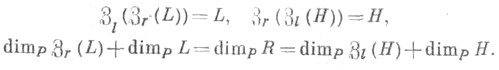

Ф. а., по существу, появились впервые в работах Г. Фробениуса [3].

Лит.:[1] Кэртис Ч., Райнер И., Теория представлений конечных групп и ассоциативных алгебр, пер. с англ., М., 1969; [2] Фейс К., Алгебра: кольца, модули и категории, пер. с англ., т. 1-2, М., 1977-79; [3] Frоbenius G., лSitzungsber. Konigl. Preuss. Akad. Wiss.