ГРАССМАНА МНОГООБРАЗИЕ

множество всех -мерных подпространств в n-мерном векторном пространстве Vнад телом k. Если k - поле, то с помощью грассмановых координат (см. Внешняя алгебра).вкладывается в -мерное проективное пространство над kв виде компактного алгебраич. многообразия. В изучении геометрич. свойств Г. м. большую роль играют так наз. многообразия Шуберта a_m=<n определяемые следующим образом: если 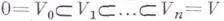- флаг подпространств, т. е. набор таких подпространств, что то

любое -мерное алгебраич. подмногообразие в Г. м. 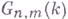эквивалентно единственной целочисленной линейной комбинации многообразий где

(см. [1]).

В случаях, когда k - поле действительных чисел , поле комплексных чисел или тело кватернионов , Г. м. над kможно рассматривать как компактное аналитич. многообразие (действительное при и 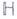и комплексное при ). Эти многообразия замечательны тем, что являются классифицирующими пространствами для классических групп соответственно. Точнее, для любого клеточного комплекса Х размерности , где соответственно, множество классов изоморфных m- мерных векторных расслоений над kс базой Xнаходится в естественном взаимно однозначном соответствии с множеством гомотопич. классов непрерывных отображений (см. [2]). Аналогичная теория для групп 'и 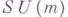приводит к рассмотрению Г. м. 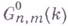( или ) ориентированных m-мерных подпространств в . Перечисленные Г. м. тесно связаны, в частности, с теорией характеристических классов.

Роль, к-рую играют Г. м. в топологии, потребовала детального изучения их топологич. инвариантов. Старейший метод этого изучения основан на многообразиях Шуберта, с помощью к-рых легко построить клеточное разбиение для 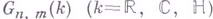. Оказывается, в частности, что циклы 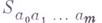порождают базисы групп гомологии Хорошо изучены также алгебры кого-мологий Г. м. и действие степеней Стинрода на них [3].

Другой аспект теории Г. м. состоит в том, что они являются однородными пространствами линейной группы над соответствующим телом и представляют собой основные примеры неприводимых симметрических пространств.

Многообразия, аналогичные Г. м., можно конструировать также из подпространств бесконечномерных векторных пространств. В частности, в теории деформаций аналитич. структур существенную роль играет банахово аналитич. многообразие , элементами к-рого являются замкнутые подпространства банахова пространства Внад , допускающие замкнутое прямое дополнение.

Лит.:[1]Ходж В., Пидо Д., Методы алгебраической геометрии, пер. с англ., т. 2, М., 1954; [2] Хьюзмоллер Д., Расслоенные пространства, пер. с англ., М., 1970; [3] Расслоенные пространства и их приложения, М., 1958; [4] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961. А. Л. Онищик.