КАРТАНА МЕТОД ВНЕШНИХ ФОРМ

- дифференциально-алгебраический метод исследования систем дифференциальных уравнений и многообразий с различными структурами. Алгебраич. основу метода составляет алгебра Грассмана. Пусть Vесть 2ⁿ -мерное векторное пространство над произвольным полем Кс базисными векторами е ⁰, е ⁱ, е ^ij, е ^ijk, ..., е ^12...n, i<j<k. Кроме векторов базиса для произвольного натурального числа q, определяются векторы е ^i1i2....iq ,i₁ i₂,.. ., i_q=1, 2,. .., n, по следующему закону: если среди натуральных чисел i₁, i₂,. .., i_q есть хотя бы одна пара одинаковых, то е ^i1...iq=0; если все числа i₁, ..., i_q попарно различны и числа j₁<j₂<...<j_q являются перестановкой чисел i₁, i₂,..., i_q, то когда подстановка (i_k)+(j)_k -четная, и е ^i1....iq=- е ^j1....jq, когда эта подстановка нечетная. В векторном пространстве Vвводится внешнее умножение:

при этом требуется выполнение обычных для гиперкомплексной системы (алгебры) законов. Построенная алгебра ранга 2" наз. алгеброй Грассмана. Вектор

наз. мономом степени р,. Сумма мономов одинаковой степени р>1 наз. внешней формой степени р;сумма мономов первой степени наз. линейной формой. Элементы поля Кявляются, по определению, формами нулевой степени. Векторы е ⁱ и любые пих линейно независимых комбинаций

образуют линейный базис алгебры Грассмана. Здесь и в дальнейшем по одинаковым индексам, встречающимся один раз снизу и один раз сверху, производится суммирование в соответствующих пределах.

Алгебраической производной 1-го порядка от внешней формы

степени рпо символу е ⁱ наз. форма степени р-1, к-рая получается из формы W_p заменой нулем всех мономов, не содержащих символа е ⁱ, и заменой единицей символа е ⁱ в остальных мономах после перенесения символа е ⁱ на первое место с соблюдением закона антикоммутативности при каждой последовательной перестановке. Ассоциированной системой линейных форм внешней формы W_p наз. совокупность всех ненулевых алгебраических производных (р-1)-го порядка от формы W_p. Рангом внешней формы W_p наз. ранг ее ассоциированной системы. Он совпадает с минимальным числом линейных форм, через к-рые, используя операцию внешнего умножения, можно выразить форму W_p. Для исследования системы дифференциальных уравнений в Rⁿ используется дифференциальная алгебра Грассмана, когда в качестве Крассматриьается множество аналитич. функций от пдействительных переменных х ⁱ, определенных в нек-рой области пространства Rⁿ, а векторы е ⁱ обозначаются символами dxⁱ. Линейные формы в ней наз. 1-формами, или формами Пфаффа. В них символы dxⁱ являются дифференциалами переменных х ⁱ. Внешние формы степени р>1 наз. р-формами, или внешними дифференциальными формами степени р. Внешним дифференциалом р-формы

наз. (р+1)-форма

Внешнее дифференцирование обладает следующими свойствами:

где - произвольные р-формы, a W_q - произвольная q-форма.

Форма Пфаффа w= a_idxⁱ тогда и только тогда является полным дифференциалом нек-рой функции f, когда ее внешний дифференциал равен нулю. Пусть

- произвольная система линейно независимых уравнений Пфаффа cm независимыми переменными х ^а и r неизвестными функциями z^p. Система Dq^a=0 наз. замыканием системы (1). Замыкание наз,. чистым замыканием (обозначается если в нем алгебраически учтена исходная система (1), то есть если в квадратичные формы Dq^a. подставлены значения dz^a из уравнений (1). Система q^a=0, Dq^a=0 или эквивалентная ей система q^a = 0,наз. замкнутой системой. Система (1) тогда и только тогда вполне интегрируема, когда Приравнивая нулю алгебраические производные от по dx^a и dz^x a=l, . .., т,x=s+l, ..., r, и присоединяя уравнения Пфаффа к исходной системе (1), получают вполне интегрируемую систему уравнений, к-рая наз. характеристической системой системы (1). Множество ее независимых первых интегралов образует наименьшую совокупность переменных, через к-рые можно выразить все уравнения системы (1). Пусть - результат подстановки в алгебраич. производную вместо dx^a, dz^x. произвольных переменных h=i, 2,..., т-1. С системой (1) ассоциируется последовательность матриц

Числа

наз. характерами, число

Q=s₁ +2s₂ +... + ms_m

наз. числом Картана системы (1). Присоединяя к замкнутой системе q^a=О, уравнения dzx= где - новые неизвестные функции, получают первое продолжение системы (1). Пусть N- число функционально независимых функций из всегда Если N=Q, то система (1) - в инволюции и ее общее решение зависит от s_m произвольных функций т аргументов, s_m-1 функций т-1 аргумента, и т. д., s₁ функций одного аргумента и sпроизвольных постоянных. Если же N<Q, то систему (1) надо продолжать, причем в результате конечного числа продолжений получается либо система в инволюции, либо противоречивая система.

Пусть, напр., имеется система

dz₁ = udx+x² dy, dz₂ = udy+у ²dx

с независимыми переменными х, у и неизвестными функциями u, z₁, z₂ (s=2, m=2, r=3). Чистое замыкание ее имеет вид:

Для этой системы:

Система не находится в инволюции. Продолженная система

dz₁ = и dx+x² dy, dz₂ = u dy+у ² dx, du = 2(y dx+x dy )вполне интегрируема и ее общее решение имеет вид:

u = 2xy+c₁,z₁ = x(xу + с ₁)+с ₂, z₂ = у( ху+ с ₁) + с ₃,

где c₁, c₂, с ₃- произвольные постоянные.

Использование К. м. в. ф. значительно упрощает формулировки и доказательства многих теорем математики и теоретич. механики. Напр., теорема Остроградского записывается формулой

где М- аналитическое ориентируемое (m+1)-мерное многообразие, Г - его m-мерная гладкая граница, W - m-форма, а DW- ее внешний дифференциал. Формула замены переменных в кратном интеграле

при отображении р: определенном формулами xⁱ= jⁱ (u¹, u²,..., и ^п), где D,получается непосредственной заменой переменных х ⁱ и их дифференциалов Так как

то

К. м. в. ф. широко применяется при исследовании многообразий с различными структурами. Пусть М- дифференцируемое многообразие класса F=- множество дифференцируемых функций на

М, D¹- множество всех векторных полей на М, U_s- множество кососимметричных F-полилинейных отображений модуля D¹...D¹(sраз,- натуральное число).

Пусть = F, а через U обозначена прямая сумма F- модулей

Элементы модуля U наз. внешними дифференциальными формами на М; элементы модуля наз. s-формами. Пусть тогда 'внешнее умножение определится формулами:

где S_r+s- группа подстановок множества 1, 2,..., r+s, а e(s)=1 или -1, в зависимости от того, четной или нечетной подстановкой является а. Модуль U кососимметрических F-полилинейных функций с внешним умножением наз. алгеброй Грассмана над многообразием М. Если Мсовпадает с Rⁿ, то получается рассмотренная выше дифференциальная алгебра Грассмана. Внешним дифференцированием наз. R-линейное отображение D: обладающее следующими свойствами: для каждого если то Df есть 1-форма, определенная равенством Df(X)=X(f), где

если Пусть, напр., М- многообразие с заданной аффинной связностью. Аффинная связность на многообразии М- это правило С, к-рое сопоставляет каждому линейное отображение Сx векторного пространства D¹ в себя, удовлетворяющее следующим двум условиям:

для f, Оператор наз. ковариантной производной относительно X. Пусть Ф - диффеоморфизм многообразия М, - аффинная связность на М. Формула

где определяет на Мновую аффинную связность. Аффинная связность наз. инвариантной относительно Ф, если В этом случае Ф наз. аффинным преобразованием многообразия М. Пусть

для всех и пусть D₁- модуль, двойственный F-модулю D¹. F -полилинейное отображение (со, X, Y)w(T(Х, Y)), где - форма Пфаффа, наз. тензорным полем кручения и обозначается через Т; F -полилинейное отображение (w, Z, X, Y)w (R(X, Y) -Z )наз. тензорным полем кривизны и обозначается через R. Пусть и Х ₁,..., Х _п - базис для векторных полей в нек-рой окрестности U_p точки р. Функции определяются на U_p формулами

Для 1-форм определенных на U _р формулами

справедливы структурные уравнения Картана:

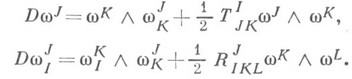
Система уравнений Пфаффа

задает m-мерное подмногообразие Продолжая эту систему с использованием структурных уравнений Картана, получают последовательность фундаментальных геометрич. объектов подмногообразия

первого, второго и т. д. порядков. В общем случае существует фундаментальный геометрич. объект

конечного порядка к, определяющий подмногообразие с точностью до постоянных. При исследовании подмногообразий многообразия МК. м. в. ф. обычно используется совместно с методом подвижного репера (см., напр., [4]).

Метод назван по имени Э. Картана (Е. Cartan), к-рый широко использовал внешние формы с 1899.

Лит.:[1] Картан Э., Внешние дифференциальные системы и их геометрические приложения, пер. с франц., М., 1962; [2] Фиников С. П., Метод внешних форм Картана в дифференциальной геометрии, М.- Л., 1948; [3] Xелгасон С, Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [4] Картан Э., Риманова геометрия в ортогональном репере, пер. с франц., М., I960.

В. С. Малаховский.