ФЛАГ

типа v в n-мерном векторном пространстве V - такой набор линейных подпространств V₁, V₂, ..., V_k в V размерностей соответственно n₁, п ₂, ..., n_k, что (здесь v = (n₁ ... ...,n_k), 0<n₁<n₂<...<n_k<п). Флаг типа v₀=(1,2,...,n-1) наз. полным флагом. Любые два флага одного и того же типа переводятся друг в друга нек-рыми линейными преобразованиями пространства V, т. <е. множество F_v(V) всех флагов типа v в F является однородным пространством полной линейной группы GL(V). Унимодулярная группа SL(V)тоже транзитивно действует на многообразии флагов F_v(V). При этом стационарная подгруппа Н _F флага Fв группе GL(V)(а также в группе SL(V))является параболич. подгруппой в GL(V) (соответственно в SL(V)). Если F - полный флаг в V, определяемый подпространствами 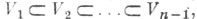то Н _F- полная треугольная подгруппа в GL(V)(соответственно в SL(V))относительно такого базиса e₁, e₂, ...., е _п пространства V, что i =l,2, ..., п. Вообще, факторпространства линейных алгебраич. групп по параболич. подгруппам иногда наз. флаговыми многообразиями. При k=1флаг типа (n₁) - это просто n₁ -мерное линейное подпространство в Vи F_(n1)(V) -Грассмана многообразие G_n,n1. В частности, F₍₁₎(V)- проективное пространство, ассоциированное с векторным пространством V. Каждое многообразие флагов F_v(V)канонич. образом снабжается структурой проективного алгебраич. многообразия (см. [1]). Если V - действительное или комплексное векторное пространство, то все многообразия F_v(V)компактны. Известны (см. [3]) клеточные разбиения и кольца когомологий многообразий F_v(V)(см. также Брюа разложение).

Лит. см. при статье Флаговая структура.
Д. В. Алексеевский.