ГЛАВНОЕ ОДНОРОДНОЕ ПРОСТРАНСТВО
- ГЛАВНОЕ ОДНОРОДНОЕ ПРОСТРАНСТВО
- главный G-объект в категории алгебраич. многообразий или схем. Если S - схема, а Г - схема групп над S, то главный G-объект в категории схем над Г наз. Г. о. п. над S. В случае, когда S - спектр поля kи Г - алгебраическая k-группа, Г. о. п. над Г есть алгебраическое k-многообразие V, на к-ром Г действует (слева), и при замене k на его сепарабельное алгебранч. замыкание  каждая точка
каждая точка 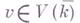 определяет изоморфное отображение
определяет изоморфное отображение  многообразий
многообразий  и
и 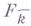 . Г. о. п. Vтривиально тогда и только тогда, когда V(k).не пусто. Множество классов, изоморфных Г. о. п., над гладкой алгебранч. группой Г может быть отождествлено с множеством Галуа когомологий
. Г. о. п. Vтривиально тогда и только тогда, когда V(k).не пусто. Множество классов, изоморфных Г. о. п., над гладкой алгебранч. группой Г может быть отождествлено с множеством Галуа когомологий (k, Г). В общем случае множество классов Г. о. п. над S-схемой групп Г совпадает с множеством одномерных неабелевых когомологий
(k, Г). В общем случае множество классов Г. о. п. над S-схемой групп Г совпадает с множеством одномерных неабелевых когомологий 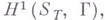 где
где 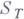 - некоторая топология Гротендика на схеме S[2].
- некоторая топология Гротендика на схеме S[2].
В ряде случаев Г. о. п. вычислено. Если k - конечное поле, то каждое Г. о. п. над связной алгебраической k-группой является тривиальным (теорема Ленга). Это же утверждение верно, если k - поле р-адических чисел, а Г - односвязная и полупростая группа (теорема Кнезера). Если  - мультипликативная S-схема групп, то множество классов Г. о. п. над Г совпадает с Пикара группой
- мультипликативная S-схема групп, то множество классов Г. о. п. над Г совпадает с Пикара группой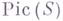 схемы S. В частности, если S - спектр поля, то эта группа тривиальна. Если
схемы S. В частности, если S - спектр поля, то эта группа тривиальна. Если 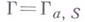 - аддитивная S- схема групп, то множество классов Г. о. п. над Г совпадает с группой
- аддитивная S- схема групп, то множество классов Г. о. п. над Г совпадает с группой 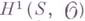 одномерных когомологий структурного пучка
одномерных когомологий структурного пучка  схемы S. В частности, это множество тривиально, если S - аффинная схема. В случае, когда k - глобальное поле (т. е. поле алгебраич. чисел или поле алгебраич. функций от одного переменного), изучение множества классов Г. о. п. над алгебраической k-группой Г основано на исследовании множества Тейта - Шафаревича III (Г), состоящего из Г. о. п. над Г, имеющих рациональные точки во всех пополнениях
схемы S. В частности, это множество тривиально, если S - аффинная схема. В случае, когда k - глобальное поле (т. е. поле алгебраич. чисел или поле алгебраич. функций от одного переменного), изучение множества классов Г. о. п. над алгебраической k-группой Г основано на исследовании множества Тейта - Шафаревича III (Г), состоящего из Г. о. п. над Г, имеющих рациональные точки во всех пополнениях 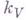 относительно нормировании поля k. В случае, когда Г - абелева группа над полем k, множество классов Г. о. п. над Г образует группу (см. Вейля - Шатле группа).
относительно нормировании поля k. В случае, когда Г - абелева группа над полем k, множество классов Г. о. п. над Г образует группу (см. Вейля - Шатле группа).
Лит.: [1] Серр Ж.-П., Когомологий Галуа пер с франц М., 1968; [2] Dem azure M., Gabriel P., Groupes algebriques, t. 1, P.-Amst., 1970; [3] Lang S., Tate J "Amer. J. Math.", 1958, v. 80, p. 659 - 84.
В. Е. Воскресенский, И. В. Долгачев.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ГЛАВНОЕ ОДНОРОДНОЕ ПРОСТРАНСТВО" в других словарях:
ГЛАВНОЕ РАССЛОЕНИЕ — расслоение такое, что группа Gдействует свободно и совершенно на пространстве X. Значение Г. р. состоит в том, что оно позволяет строить ассоциированные (с ним) расслоения со слоем F, если задано представление Gв группе гомеоморфизмов F.… … Математическая энциклопедия
ГЛАВНЫЙ G-ОБЪЕКТ — в топологизированной категории понятие теории категорий, частные случаи которого главное расслоение втопологии, главное однородное пространство в алгеб раич. геометрии и др. Пусть G групповой объект категории С с произведениями и финальным… … Математическая энциклопедия
ЭЛЛИПТИЧЕСКАЯ КРИВАЯ — неособая полная алгебраическая кривая рода 1. Теория Э. к. является истоком большей части современной алгебраич. геометрии. Но исторически теория Э. к. возникла как часть анализа, как теория эллиптических интегралов и эллиптических функций.… … Математическая энциклопедия
ФЛОРЕНСКИЙ — Павел Александрович (1882 1937) православный мыслитель, ученый, представитель серебряного века отеч. культуры. Получил светское (физико мат. отделение Моск. ун та) и духовное (Моск. духовная академия) образование. Защитил магистерскую дис … Энциклопедия культурологии
ПОДВИЖНОГО РЕПЕРА МЕТОД — дифференциально геометрический метод локального исследования подмногообразий различных однородных пространств, исходным моментом к poro является отнесение самого подмногообразия и всех его геометрич. объектов к возможно более общему (подвижному)… … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНО-ГЕОМЕТРИЧЕСКАЯ СТРУКТУРА — одно из основных понятий современной дифференииальной геометрии, включающее конкретные изучаемые в ней структуры. Д. г. с. определяется для данного дифференцируемого многообразия М п как дифференцируемое сечение в расслоенном пространстве( Х F,… … Математическая энциклопедия
ПСЕВДОГРУППОВАЯ СТРУКТУРА — на многообразии M максимальный атлас Агладких локальных диффеоморфизмов многообразия Мна фиксированное многообразие V, все функции перехода между к рыми принадлежат данной псевдогруппе Г локальных преобразований многообразия V. Псевдогруппа Г наз … Математическая энциклопедия
Финляндия* — Содержание: I. Физический очерк. II. Население. III. Экономический обзор. IV. Финансы. V. Управление и судоустройство. VI. Финские войска и воинская повинность. VII. Образование. VIII. Наука, искусство, печать и общественная жизнь. IX. Церковь. X … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Финляндия — I Содержание [Историю Финляндии, историю литературы, язык и мифологию см. соотв. разделы.]. I. Физический очерк. II. Население. III. Экономический обзор. IV. Финансы. V. Управление и судоустройство. VI. Финские войска и воинская повинность. VII.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Ломоносов, Михаил Васильевич — — ученый и писатель, действительный член Российской Академии Наук, профессор химии С. Петербургского университета; родился в дер. Денисовке, Архангельской губ., 8 ноября 1711 г., скончался в С. Петербурге 4 апреля 1765 года. В настоящее… … Большая биографическая энциклопедия
 каждая точка
каждая точка 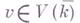 определяет изоморфное отображение
определяет изоморфное отображение  многообразий
многообразий  и
и 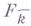 . Г. о. п. Vтривиально тогда и только тогда, когда V(k).не пусто. Множество классов, изоморфных Г. о. п., над гладкой алгебранч. группой Г может быть отождествлено с множеством Галуа когомологий
. Г. о. п. Vтривиально тогда и только тогда, когда V(k).не пусто. Множество классов, изоморфных Г. о. п., над гладкой алгебранч. группой Г может быть отождествлено с множеством Галуа когомологий (k, Г). В общем случае множество классов Г. о. п. над S-схемой групп Г совпадает с множеством одномерных неабелевых когомологий
(k, Г). В общем случае множество классов Г. о. п. над S-схемой групп Г совпадает с множеством одномерных неабелевых когомологий 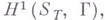 где
где 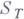 - некоторая топология Гротендика на схеме S[2].
- некоторая топология Гротендика на схеме S[2]. - мультипликативная S-схема групп, то множество классов Г. о. п. над Г совпадает с Пикара группой
- мультипликативная S-схема групп, то множество классов Г. о. п. над Г совпадает с Пикара группой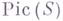 схемы S. В частности, если S - спектр поля, то эта группа тривиальна. Если
схемы S. В частности, если S - спектр поля, то эта группа тривиальна. Если 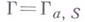 - аддитивная S- схема групп, то множество классов Г. о. п. над Г совпадает с группой
- аддитивная S- схема групп, то множество классов Г. о. п. над Г совпадает с группой 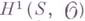 одномерных когомологий структурного пучка
одномерных когомологий структурного пучка  схемы S. В частности, это множество тривиально, если S - аффинная схема. В случае, когда k - глобальное поле (т. е. поле алгебраич. чисел или поле алгебраич. функций от одного переменного), изучение множества классов Г. о. п. над алгебраической k-группой Г основано на исследовании множества Тейта - Шафаревича III (Г), состоящего из Г. о. п. над Г, имеющих рациональные точки во всех пополнениях
схемы S. В частности, это множество тривиально, если S - аффинная схема. В случае, когда k - глобальное поле (т. е. поле алгебраич. чисел или поле алгебраич. функций от одного переменного), изучение множества классов Г. о. п. над алгебраической k-группой Г основано на исследовании множества Тейта - Шафаревича III (Г), состоящего из Г. о. п. над Г, имеющих рациональные точки во всех пополнениях 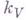 относительно нормировании поля k. В случае, когда Г - абелева группа над полем k, множество классов Г. о. п. над Г образует группу (см. Вейля - Шатле группа).
относительно нормировании поля k. В случае, когда Г - абелева группа над полем k, множество классов Г. о. п. над Г образует группу (см. Вейля - Шатле группа).