- Косое произведение векторов
-
Псевдоскалярное или косое произведение векторов
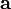 и
и 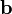 на плоскости называют число
на плоскости называют числогде
 — угол вращения (против часовой стрелки) от
— угол вращения (против часовой стрелки) от 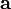 к
к 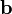 . Если хотя бы один из векторов
. Если хотя бы один из векторов 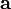 и
и 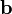 нулевой, то полагают
нулевой, то полагают  .
.Записывается с помощью тензора Леви-Чивиты
 через координаты векторов так:
через координаты векторов так:Свойства
 .
. является псевдоскаляром, то есть инвариантом при всех невырожденных изометриях, не включающих отражений.
является псевдоскаляром, то есть инвариантом при всех невырожденных изометриях, не включающих отражений.- Псевдоскалярное произведение
 — это ориентированная площадь параллелограмма, натянутого на векторы
— это ориентированная площадь параллелограмма, натянутого на векторы 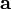 и
и 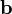 .
.
- Абсолютная величина псевдоскалярного произведения
 — это площадь такого параллелограмма.
— это площадь такого параллелограмма. - Ориентированная площадь треугольника
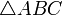 выражается формулой
выражается формулой
- а его площадь, следовательно, равна модулю этой величины.
- Абсолютная величина псевдоскалярного произведения
- Если рассмотривать плоскость в трёхмерном пространстве, то
- где «
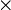 » и «
» и « » соответственно — векторное и скалярное произведение, а
» соответственно — векторное и скалярное произведение, а 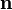 — единичный вектор нормали к плоскости. Знак плюс берется в случае, если правый базис на плоскости, дополненный вектором
— единичный вектор нормали к плоскости. Знак плюс берется в случае, если правый базис на плоскости, дополненный вектором 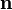 образует также правый базис; в противном случае минус.
образует также правый базис; в противном случае минус.
 — необходимое и достаточное условие параллельности (или антипараллельности) векторов на плоскости.
— необходимое и достаточное условие параллельности (или антипараллельности) векторов на плоскости.
См. также
Ссылки
Wikimedia Foundation. 2010.




