ДИСКРЕТНОГО НОРМИРОВАНИЯ КОЛЬЦО

ДИСКРЕТНОГО НОРМИРОВАНИЯ КОЛЬЦО

дискретно нормированное кольцо,- кольцо с дискретным нормированием, т. е. область целостности с единицей, в к-рой существует такой элемент я, что любой ненулевой идеал порождается нек-рой степенью элемента я; такой элемент наз. униформизирующим и определен с точностью до умножения на обратимый элемент. Каждый ненулевой элемент Д. н. к. единственным способом записывается в виде upn, где и- обратимый элемент, а - целое. Примерами Д. н. к. являются кольцо Z р целых р-адических чисел, кольцо к[[Т]]. формальных степенных рядов от одной переменной Тнад полем к, кольцо Bumma векторов W(k)для совершенного поля к.

Д. н. к. может быть определено также как: локальное кольцо главных идеалов; локальное дедекиндово кольцо; локальное одномерное кольцо Крулля; локальное нётерово кольцо с главным максимальным идеалом; нётерово кольцо нормирования; кольцо нормирования с группой значений Z.

Пополнение (в естественной топологии локального кольца) Д. н. к. снова есть Д. н. к. Дискретно нормированное кольцо компактно тогда и только тогда, когда оно полно, а его поле вычетов конечно; любое такое кольцо либо изоморфно k[[Т]], где к- конечное поле, либо является конечным расширением Z р..

Если - локальный гомоморфизм Д. н. к. с

униформизирующими p и П, то p=uП e, где и- обратимый элемент в В. Целое число е=е( В/А )наз. индексом ветвления расширения а наз. степенью вычетов. Такая ситуация возникает, когда рассматривают целое замыкание Вкольца дискретного нормирования Ас полем частных Кв конечном расширении Lполя К. В этом случае Весть полулокальное кольцо главных идеалов, и если n1, ... , ns- его максимальные идеалы, то Bi= Bn являются Д. н. к. Если предположить, что L- сепарабельное расширение Кстепени п, то верна формула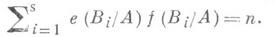

Если L/K есть расширение Галуа, то все е( В,/А )и все f(Bi/A )равны между собой, и n=sef. Если же А- полное Д. н. к., то уже само Вбудет Д. н. к., и е( В/А) f(B/A)=n. В этих предположениях расширение 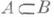(а также Lнад К)наз. неразветвленным расширением, если е( В/А)=1, а поле В/п сепарабельно над А/m;слабо разветвленным, если е( В/А )взаимно просто с характеристикой поля А/m, а В/nсепарабельно над А/т;вполне разветвленным, если f(B/A)=i.

Теория модулей над Д. н. к. имеет большое сходство с теорией абелевых групп (см. [3]). Любой модуль конечного типа есть прямая сумма циклич. модулей; модуль без кручения является плоским модулем; любой проективный модуль или подмодуль свободного модуля свободен. Однако прямое произведение бесконечного числа свободных модулей не свободно. Модуль без кручения счетного ранга над полным Д. н. к. является прямой суммой модулей ранга 1.

Лит.:[1] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971; [2] Алгебраическая теория чисел, пер. с англ., М., 1969; [3] Карla nskу J., "Trans. Amer. Math. Soc", 1952, v. 72, p. 327 - 40.

Б. И. Данилов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "ДИСКРЕТНОГО НОРМИРОВАНИЯ КОЛЬЦО" в других словарях:

  • ДЕДЕКИНДОВО КОЛЬЦО — ассоциативное коммутативное кольцо Rс единицей, не содержащее делителей нуля (т. е. коммутативная область целостности), в к ром каждый собственный идеал представим в виде произведения простых идеалов (идеал Ркольца R наз. простым, если… …   Математическая энциклопедия

  • ЛОКАЛЬНОЕ КОЛЬЦО — коммутативное кольцо с единицей, имеющее единственный максимальный идеал. Если А Л. к. с максимальным идеалом то факторкольцо является полем и наз. полем вычетов Л. к. А. Примеры Л. к. Любое поле или кольцо нормирования является локальным.… …   Математическая энциклопедия

  • РЕГУЛЯРНОЕ КОЛЬЦО — в к о м м у т а т и в н о й а л г е б р е нётерово кольцо А, все локализации к рого регулярны; здесь простой идеал в А. При этом локальное нётерово кольцо Ас максимальным идеалом наз. р е г у л я р н ы м, если порождается пэлементами, где n=dim A …   Математическая энциклопедия

  • КРУЛЛЯ КОЛЬЦО — коммутативное целостное кольцо А, для к poro существует семейство дискретных нормировании поля частных Ккольца А, удовлетворяющее следующим условиям: а) для любого н для всех i, исключая, быть может, конечное число, б) для условие эквивалентно… …   Математическая энциклопедия

  • НОРМИРОВАНИЕ — логарифмическое нормирование, оценка поля, отображение поля Кв где Г линейно упорядоченная абелева группа, а присоединяемый элемент считается больше любого элемента из группы и для любого . При этом Н. должно удовлетворять следующим условиям:… …   Математическая энциклопедия

  • p-АДИЧЕСКОЕ ЧИСЛО — элемент расширения поля рациональных чисел, получаемого на основе свойств делимости целых чисел на заданное простое число р. Это расширение есть пополнение поля рациональных чисел относительно неархимедова нормирования (см. Абсолютное значение).… …   Математическая энциклопедия

  • ВИТТА ВЕКТОР — элемент алгебраич. конструкции, впервые предложенной Э. Впттом в 1936 [1] в связи с описанием неразветвленных расширений полей р адических чисел. Позже В. в. были применены при изучении алгебраических многообразий над полем положительной… …   Математическая энциклопедия

  • ДИВИЗОР — обобщение понятия делителя элемента коммутативного кольца. Впервые (под назв. идеальный делитель ) это понятие возникло в работах Э. Куммера [1] об арифметике круговых полей. Теория Д. для коммутативного кольца А с единицей без делителей нуля… …   Математическая энциклопедия

  • ДИСКРЕТНОЕ НОРМИРОВАНИЕ — нормирование тела, группа значений к рого изоморфна группе целых чисел Z. В этом случае кольцо нормирования является дискретного нормирования кольцом. Иногда Д. н., точнее Д. н. высоты (или ранга) r, наз. нормирование, имеющее группой значений r… …   Математическая энциклопедия

  • УНИФОРМИЗУЮЩИЙ ЭЛЕМЕНТ — элемент p дискретно нормированного кольца Ас простым идеалом р такой, что Если p1, p2 два У. э. в А , то элемент обратим в А. Пусть R нек рая система представителей в Аэлементов поля вычетов Тогда любой элемент однозначно записывается в виде… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»