АНАЛИТИЧЕСКОЕ КОЛЬЦО

АНАЛИТИЧЕСКОЕ КОЛЬЦО

кольцо ростков аналитич. функций в точке аналитического пространства. Более точно: пусть kесть поле с нетривиальным абсолютным значением (обычно предполагаемое полным) и 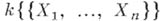есть fc-алгебра степенных рядов от с коэффициентами в k, сходящихся в нек-ром полицилиндре с центром (при этом каждый ряд сходится в своем полицилиндре). Аналитическим кольцом над k, или аналитической k-a лгеброй, наз. факторкольцо кольца 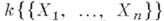; обычно k - поле R действительных или поле С комплексных чисел. Каждое А. к. является локальным, нётеровым и гензелевым кольцом; его поле вычетов изоморфно k. А. к. будет регулярным (и факториальным) кольцом, а его пополнение в топологии, определяемой максимальным идеалом , совпадает с кольцом формальных степенных рядов 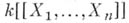. Для А. к. верна нормализационная лемма: целостное А. к. является конечным расширением А. к. Вообще, алгебры, конечные над , наз. кваз и аналитическими k- алгебрами. Еслп - совершенное поле, то А. к. является превосходным кольцом.

Лит.:[1] Dieudonne J., Grothendieck A "J. Algebra", 1967, у. 5, № 3, р. 305-24; [2] Мальгранж Б. Идеалы дифференцируемых функций, пер. с англ., М., 1968; [3] Abhyankar S. S., Local analytic geometry, N. Y 1964. В. И. Данилов.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно решить контрольную?

Полезное


Смотреть что такое "АНАЛИТИЧЕСКОЕ КОЛЬЦО" в других словарях:

  • НОРМАЛЬНОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО — аналитическое пространство, локальные кольца всех точек к рого нормальны, т. е. являются цело вамкнутыми областями целостности. Точка ханалитич. пространства Xназ. нормальной (говорят также, что Xнормально в точке х), если локальное кольцо… …   Математическая энциклопедия

  • НЕПРИВОДИМОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО — аналитическое пространство, к рое нельзя представить в виде объединения локально конечного семейства его аналитич. одпространств. Н. а. п. является обобщением понятия неприводимого аналитического множества. Всякое аналитич. ространство можно… …   Математическая энциклопедия

  • Внутреннее транспортное кольцо Челябинска — Внутреннее транспортное кольцо Челябинска …   Википедия

  • философия языка — Аналитическое движение в Кембридже и Оксфорде Аналитическая философия в Кембридже     Философия языка развивалась в двух центрах Кембридже и Оксфорде, поэтому ее и называют «кембридж оксфордской философией». Она развивалась скорее как движение, а …   Западная философия от истоков до наших дней

  • Ленинградский трамвай — Санкт петербургский трамвай Трамвайная система Страна: Россия Город: Санкт Петербург Тип системы: пассажирская, с 1914 по 1997 пассажирско грузовая Дата откры …   Википедия

  • Памятник пуска Петербургского трамвая — Санкт петербургский трамвай Трамвайная система Страна: Россия Город: Санкт Петербург Тип системы: пассажирская, с 1914 по 1997 пассажирско грузовая Дата откры …   Википедия

  • Памятник пуска первого петербургского трамвая — Санкт петербургский трамвай Трамвайная система Страна: Россия Город: Санкт Петербург Тип системы: пассажирская, с 1914 по 1997 пассажирско грузовая Дата откры …   Википедия

  • Петербургская трамвайная сеть — Санкт петербургский трамвай Трамвайная система Страна: Россия Город: Санкт Петербург Тип системы: пассажирская, с 1914 по 1997 пассажирско грузовая Дата откры …   Википедия

  • Петербургский трамвай — Санкт петербургский трамвай Трамвайная система Страна: Россия Город: Санкт Петербург Тип системы: пассажирская, с 1914 по 1997 пассажирско грузовая Дата откры …   Википедия

  • Питерский трамвай — Санкт петербургский трамвай Трамвайная система Страна: Россия Город: Санкт Петербург Тип системы: пассажирская, с 1914 по 1997 пассажирско грузовая Дата откры …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»