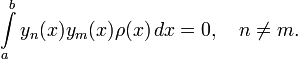- Задача Штурма-Лиувилля
-
Задача Штурма — Лиувилля состоит в отыскании нетривиальных решений на промежутке
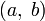 однородного уравнения
однородного уравнения- L[y] + λρ(x)y(x) = 0,
удовлетворяющих однородным граничным условиям
и значений параметра λ, при которых такие удовлетворяющие указанным граничным условиям решения существуют.
Оператор L[y] здесь — это действующий на функцию y(x) линейный дифференциальный оператор второго порядка вида
(оператор Штурма — Лиувилля). x — вещественный аргумент.
Функции
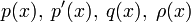 предполагаются непрерывными на
предполагаются непрерывными на 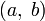 , кроме того функции
, кроме того функции 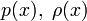 положительны на
положительны на 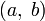 .
.Искомые нетривиальные решения называются собственными функциями этой задачи, а значения λ, при которых такое решение существует — её собственными значениями (каждому собственному значению соответствует собственная функция).
Свойства
Данная задача обладает рядом свойств:
- Существует бесконечное счетное множество {λn} собственных значений и соответствующая им бесконечная последовательность {yn(x)} собственных функций. Все собственные значения можно занумеровать в порядке возрастания их абсолютной величины
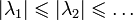
- Каждому собственному значению соответствует с точностью до постоянного множителя только одна собственная функция.
- В случае граничных условий y(a) = y(b) = 0 и при выполнении условия
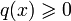 все собственные значения краевой задачи положительны λn > 0.
все собственные значения краевой задачи положительны λn > 0. - Собственные функции yn(x) образуют на
![[a,\;b]](/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) ортогональную с весом ρ(x) систему {yn(x)}:
ортогональную с весом ρ(x) систему {yn(x)}:
Wikimedia Foundation. 2010.

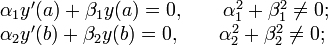
![L[y]\equiv\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right]-q(x)y(x)](/pictures/wiki/files/102/f53574127930b60938f30cffd2e70895.png)