ШТУРМА - ЛИУВИЛЛЯ ЗАДАЧА

- задача, порожденная на конечном или бесконечном интервале ( а, b) изменения переменной хуравнением

и нек-рыми граничными условиями, где р(х) и r(х) положительны, l(х)действительна, а - комплексный параметр. Начало глубокому изучению этой задачи положили Ш. Штурм (Ch. Sturm) и Ж. Лиувилль (J. Liouville). Понятия и методы, зародившиеся в процессе изучения Ш.- Л. з., сыграли большую роль в развитии многих направлений математики и физики. Она была и остается постоянным источником новых идей и задач для спектральной теории операторов и смежных вопросов анализа. Особое значение приобрела она в последнее время после открытия связи с нек-рыми нелинейными эволюционными уравнениями математич. физики.
Если р(х)дифференцируема, а р(х)r(х) - дифференцируема дважды, то уравнение (1) с помощью подстановки сводится к виду (см. [1])

Принято различать регулярные и сингулярные задачи. Ш.- Л. з. для уравнения (2) наз. рeгулярной, если интервал ( а, b) изменения переменной хконечен и если функция q(х)суммируема во всем интервале ( а, b). Если же интервал ( а, b )бесконечен или q (х)несуммируема (или и то и другое), то эта задача наз. сингулярной.
Ниже рассматриваются в отдельности следующие случаи: 1) интервал (a, b) конечен, в этом случае, не нарушая общности, можно считать, что а=0и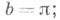 2) a = 0, 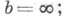3)

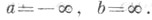
1. Рассматривается задача, порожденная на сегменте уравнением (2) и разделенными граничными условиями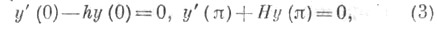
где q(х) - действительная суммируемая на сегменте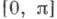 функция, hи Н - произвольные конечные или бесконечные фиксированные действительные числа, 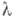- комплексный параметр. Если 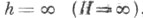, то первое (второе) условие в (3) заменяется условием у(0)=0 Для определенности далее предполагается, что числа, участвующие в граничных условиях, конечны.
Число наз. собственным значением задачи (2), (3), если при уравнение (2) имеет нетривиальное решение 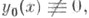удовлетворяющее граничным условиям (3); при этом функция у ₀ (х) наз. собственной функцией, соответствующей собственному значению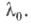
Собственные значения граничной задачи (2), (3) действительны; каждому собственному значению соответствует единственная линейно независимая собственная функция (в силу действительности q(х) и чисел h, Нсобственные функции задачи (2), (3) можно выбрать действительными); собственные функции у ₁ (х) и у ₂ (х). соответствующие различным собственным значениям, ортогональны, т. е.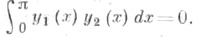

Существует неограниченно возрастающая последовательность собственных значений 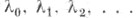граничной задачи (2). (3); при этом собственная функция у _n (х). соответствующая собственному значению имеет ровно пнулей в интервале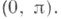
Пусть - пространство Соболева, состоящее из заданных на сегменте 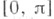комплекснозначных функций, к-рые имеют т-1 абсолютно непрерывных производных и производную порядка т, суммируемую на сегменте 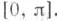Если то собственные значения 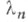граничной задачи (2), (3) при больших n удовлетворяют асимптотич. равенству (см. [4]):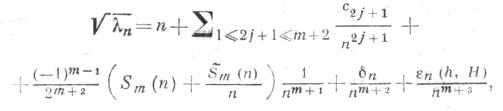

где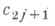 - независимые от пчисла,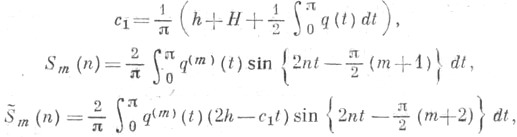

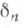не зависит от h, H и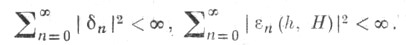

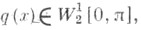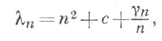Отсюда, в частности, следует, что если то где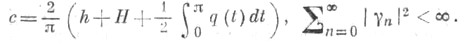

Поэтому ряд сходится. Его сумма наз. регуляризованным следом задачи (2), (3) (см. [13]):

Пусть v₀(x), v₁(x), . ..- ортонормированные собственные функции задачи (2), (3), соответствующие собственным значениям 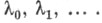Для каждой функции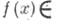 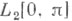имеет место так наз. равенство Парсеваля 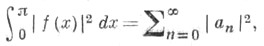где и справедлива формула разложения по собственным функциям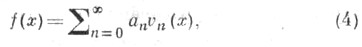

где ряд сходится в метрике пространства
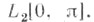
Теоремы полноты и разложения для регулярной Ш.- Л. з. впервые доказаны В. А. Стекловым [14].
Если функция f(x) имеет вторую непрерывную производную и удовлетворяет граничным условиям (3), то справедливы следующие утверждения (см. (15]):
а) ряд (4) сходится абсолютно и равномерно на сегменте к функции f(x);
б)один раз продифференцированный ряд (4) сходится абсолютно и равномерно на сегменте к f'(x);
в) в каждой точке, в к-рой f "(x) удовлетворяет какому-либо локальному условию разложения в ряд Фурье (напр., имеет ограниченную вариацию), дважды продифференцированный ряд (4) сходится к f"(x).
Для любой функции ряд (4) является равномерно равносходящнмся с рядом Фурье функции f(x) по cos nx, т. е.

где

Это утверждение означает, что разложение функции f(x)по собственным функциям граничной задачи (2), (3) сходится при тех же условиях, что и разложение f(х)в ряд Фурье по косинусам (см. [1], [4]).

2. Рассматривается дифференциальное уравнение (2) на полуоси с граничным условием в нуле: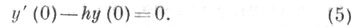

Функция q(x)предполагается действительной и суммируемой в каждом конечном подинтервале интервала а число hдействительным.
Пусть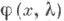 - решение уравнения (2) с начальными условиями y(0) = 1, y'(0)=h (так что 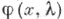удовлетворяет и граничному условию (5)). Пусть f(x) -любая функция из 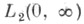и где b- произвольное конечное положительное число. Для каждой функции q(х) икаждого числа hсуществует, по крайней мере, одна, не зависящая от f(x), неубывающая функция 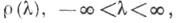обладающая следующими свойствами:
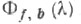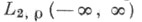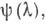а) существует функция являющаяся пределом при в метрике (пространства -измеримых функций для к-рых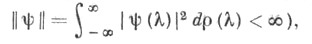

т. е.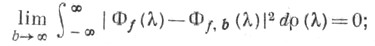

б) имеет место равенство Парсеваля

Функция 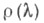наз. спектральной функцией (или спектральной плотностью) граничной задачи (2), (5) (см. [9] - [11]).
Для спектральной функции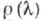 задачи (2), (5) справедлива асимптотич. формула (см. [16]) (в уточненном виде см. [17]):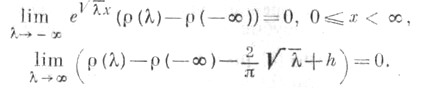

Справедлива следующая теорема равносходимости: для произвольной функции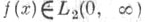 пусть

(интегралы сходятся в метриках пространств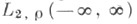 и соответственно); тогда при каждом фиксированном сходится интеграл

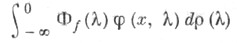
абсолютно и равномерно относительно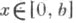 и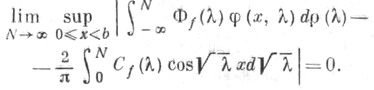

Пусть задача (2), (5) имеет дискретный спектр, т. е. ее спектр состоит из счетного числа собственных значений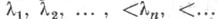 с единственной предельной точкой в бесконечности. При определенных условиях на функцию q(х)для функции 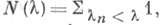т. e. числа собственных значений, меньших справедлива асимптотич. формула: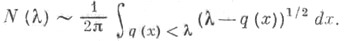

Наряду с решением вводится второе решение 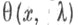уравнения (2), удовлетворяющее условиям 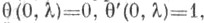так что 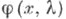и образуют фундаментальную систему решений уравнения (2). При фиксированных числах 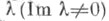и b>0 рассматривается дробно-линейная функция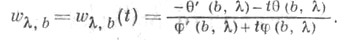

Когда независимая переменная tпробегает действительную ось, точка описывает нек-рую окружность, ограничивающую круг Он всегда лежит в той же полуплоскости (нижней или верхней), что и 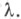С увеличением bкруг 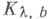сжимается, т. е. при b<b' круг лежит целиком внутри круга Существует (при предельный круг или точка 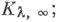при этом если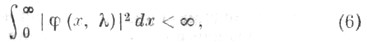

то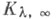 будет кругом, и точкой - в противном случае (см. [10]). Если условие (6) выполняется для одного какого-либо недействительного значения 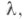то оно выполняется для всех значений В случае продельного круга для всех значений все решения уравнения (2) принадлежат пространству 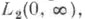а в случае предельной точки для каждого недействительного значения 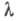это уравнение имеет решение вида 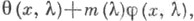принадлежаще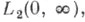е где 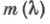- предельная точка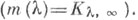
Если где с - нек-рая положительная постоянная, то имеет место случай предельной точки (см. [19]), более общие результаты см. [20], [21] .

3. Рассматривается теперь уравнение (2) на всей оси 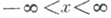при предположении, что q(x)действительная суммируемая в каждом конечном подинтервале из 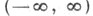функция. Пусть 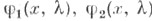- решения уравнения (2), удовлетворяющие условиям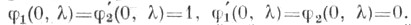

Существует, по крайней мере, одна действительная симметрическая неубывающая матрица-функция

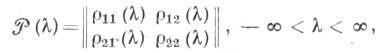
обладающая следующими свойствами:
а) для любой функции существуют функции 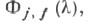j=1,2, определенные равенствами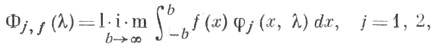

где предел - по метрике пространства
б) имеет место равенство Парсеваля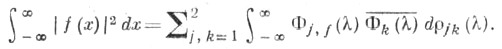

Лит.:[1] Левитан Б. М., СаргсянИ. С., Введение в спектральную теорию, М., 1970; [2] Левитан Б. М., Разложение по собственным функциям дифференциальных уравнений второго порядка, М.- Л., 1950; [3] его же, Теория операторов обобщенного сдвига, М., 1973; [4] Марченко В. А., Операторы Штурма - Лиувилля и их приложения, К., 1977; [5] Титчмарш Э. Ч., Разложения по собственным функциям, связанные с дифференциальными уравнениями второго порядка, пер. с англ., т. 1, М., 1960; [6] Коддингтоy Э. А., Левинсон Н., Теория обыкновенных дифференциальных уравнений, пер. с англ., М., 1958; [7] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [8] Костюченко А. Г., Саргсян И. С., Распределение собственных значений, М., 1979; [9] Wеуl Н., лGott. Nachr.