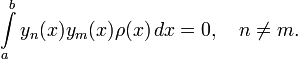- Задача Штурма — Лиувилля
-
Задача Штурма — Лиувилля
Задача Штурма — Лиувилля состоит в отыскании нетривиальных решений на промежутке
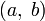 однородного уравнения
однородного уравненияудовлетворяющих однородным граничным условиям
и значений параметра
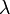 , при которых такие удовлетворяющие указанным граничным условиям решения существуют.
, при которых такие удовлетворяющие указанным граничным условиям решения существуют.Оператор
![\!L[y]](http://dic.academic.ru/pictures/wiki/files/56/864fdb22f6cab80980206423c15173c5.png) здесь — это действующий на функцию
здесь — это действующий на функцию 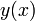 линейный дифференциальный оператор второго порядка вида
линейный дифференциальный оператор второго порядка вида(оператор Штурма — Лиувилля). x — вещественный аргумент.
Функции
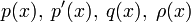 предполагаются непрерывными на
предполагаются непрерывными на 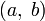 , кроме того функции
, кроме того функции 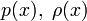 положительны на
положительны на 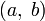 .
.Искомые нетривиальные решения называются собственными функциями этой задачи, а значения
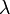 , при которых такое решение существует — её собственными значениями (каждому собственному значению соответствует собственная функция).
, при которых такое решение существует — её собственными значениями (каждому собственному значению соответствует собственная функция).Свойства
Данная задача обладает рядом свойств:
- Существует бесконечное счетное множество {λn} собственных значений и соответствующая им бесконечная последовательность {yn(x)} собственных функций. Все собственные значения можно занумеровать в порядке возрастания их абсолютной величины
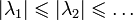
- Каждому собственному значению соответствует с точностью до постоянного множителя только одна собственная функция.
- В случае граничных условий y(a) = y(b) = 0 и при выполнении условия
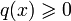 все собственные значения краевой задачи положительны λn > 0.
все собственные значения краевой задачи положительны λn > 0. - Собственные функции yn(x) образуют на
![[a,\;b]](http://dic.academic.ru/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) ортогональную с весом ρ(x) систему {yn(x)}:
ортогональную с весом ρ(x) систему {yn(x)}:
Wikimedia Foundation. 2010.
Задача Штурма-Лиувилля — Задача Штурма Лиувилля состоит в отыскании нетривиальных решений на промежутке однородного уравнения L[y] + λρ(x)y(x) = 0, удовлетворяющих однородным граничным условиям и значений параметра λ, при которых такие удовлетворяющие указанным… … Википедия
Задача Штурма — Задача Штурма Лиувилля состоит в отыскании нетривиальных (т.е. отличных от тождественного нуля) решений на промежутке однородного уравнения удовлетворяющих однородным граничным условиям и значений параметра … Википедия
ШТУРМА - ЛИУВИЛЛЯ ОБРАТНАЯ ЗАДАЧА — задача, в к рой требуется восстановить функцию (потенциал) q(x)по тем или иным спектральным характеристикам оператора А, порождённого дифференциальным выражением l[у] = y +q(x)yи нек рыми граничными условиями в гильбертовом пространстве L2(a, b) … Математическая энциклопедия
ШТУРМА -ЛИУВИЛЛЯ ЗАДАЧА — задача, порождённая на конечном или бесконечном интервале ( а, b) изменения переменной c ур нием и нек рыми граничными условиями, где положительны, действительна, а комплексный параметр. Начало глубокому изучению этой задачи положили Ш. Штурм (Ch … Физическая энциклопедия
Штурма-Лиувилля задача — Штурма ‒ Лиувилля задача, задача о нахождении отличных от нуля решений дифференциального уравнения [p (x) y ] + q (x) y = ly, (1) удовлетворяющих граничным условиям вида A1y (a) + B1y (a) = 0, А2у (b) + B2y (b) = 0 (т. н. соб … Большая советская энциклопедия
ШТУРМА - ЛИУВИЛЛЯ ЗАДАЧА — задача, порожденная на конечном или бесконечном интервале ( а, b) изменения переменной хуравнением и нек рыми граничными условиями, где р(х) и r(х) положительны, l(х)действительна, а комплексный параметр. Начало глубокому изучению этой задачи… … Математическая энциклопедия
Штурма - Лиувилля задача — задача о нахождении отличных от нуля решений дифференциального уравнения [p (x) y ] + q (x) y = λy, (1) удовлетворяющих граничным условиям вида A1y (a) + B1y (a) = 0, А2у (b) + B2y (b) = 0 (т. н.… … Большая советская энциклопедия
Краевая задача — Краевая задача дифференциальное уравнение (система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце интервала интегрирования. Решение краевой задачи ищется в виде линейной… … Википедия
Ахтямов, Азамат Мухтарович — Азамат Мухтарович Ахтямов Дата рождения: 31 марта 1962(1962 03 31) (50 лет) Место рождения: г. Уфа, Башкирская АССР, РСФСР, СССР Страна … Википедия
Султанаев, Яудат Талгатович — Яудат Талгатович Султанаев Дата рождения: 19 июля 1948(1948 07 19) (64 года) Научная сфера: математика Награды и премии … Википедия

![\!L[y]+\lambda\rho(x)y(x)=0,](http://dic.academic.ru/pictures/wiki/files/101/e2c3301ed8e0bf2d176fcdf0ad106827.png)
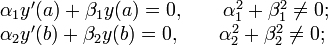
![L[y]\equiv\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right]-q(x)y(x)](http://dic.academic.ru/pictures/wiki/files/102/f53574127930b60938f30cffd2e70895.png)