- Доверительная зона
-
Теоре́ма Колмого́рова в математической статистике уточняет скорость сходимости выборочной функции распределения к её теоретическому аналогу.
Содержание
Формулировка
Пусть
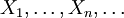 — бесконечная выборка из распределения, задаваемого непрерывной функцией распределения F. Пусть
— бесконечная выборка из распределения, задаваемого непрерывной функцией распределения F. Пусть  — выборочная функция распределения, построенная на первых n элементах выборки. Тогда
— выборочная функция распределения, построенная на первых n элементах выборки. Тогда по распределению при
по распределению при 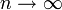 ,
,
где K — случайная величина, имеющая распределение Колмогорова.
Замечание
Неформально говорят, что скорость сходимости выборочной функции распределения к её теоретическому аналогу имеет порядок
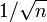 .
.Определение границ доверительной зоны
Теорема Колмогорова очень часто применяется, чтобы определить границы, в которые с заданной вероятностью попадает теоретическая функция F(x):
где kγ — квантиль уровня γ закона распределения Колмогорова.
Таким образом с вероятностью γ при
 находится в указанном интервале.
находится в указанном интервале.Вероятность γ называют уровнем значимости.
Область, определяемую этими границами, называют асимптотической γ-доверительной зоной для теоретической функции распределения.
См. также
Wikimedia Foundation. 2010.

