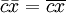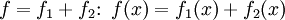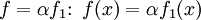Двойственное пространство
- Двойственное пространство
-
Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе — термин, применяющийся при описании двойственности линейных пространств.
Как правило, под сопряжённым пространством понимают линейно-сопряжённое пространство, т.е. пространство линейных функционалов.
Линейно-сопряжённое пространство — определение
Для линейных функционалов на линейном пространстве E можно определить операции сложения и умножения на число:
Эти определения удовлетворяют аксиомам линейного пространства. То есть, совокупность всех линейных функционалов на E также образует линейное пространство. Это пространство называется сопряжённым к E, оно обычно обозначается E * .
Свойства
- В конечномерном случае сопряжённое пространство E * имеет ту же размерность, что и пространство E.
- Если пространство E евклидово, то есть на нём определено скалярное произведение, то существует канонический изоморфизм между E и E * .
- В конечномерном случае верно также, что пространство, сопряжённое к сопряжённому E * * , совпадает с E (точнее, существует канонический изоморфизм между E и E * * ).
Обозначения
Обычно элементы пространства E обозначают вектором-строкой, а элементы E * — вектором-столбцом. В тензорном исчислении применяется обозначение xk для элементов E (верхний, или контравариантный индекс) и xk для элементов E * (нижний, или ковариантный индекс).
Трудности в бесконечномерном случае
Попытка прямо применить вышеприведённое определение в случае бесконечномерных линейных пространств приводит к неконструктивным и малополезным алгебраически сопряжённым пространствам. Для важного случая топологических линейных пространств рассматриваются топологически сопряжённые пространства, состоящие только из непрерывных функционалов. Однако, для топологического линейного сопряжения пространство, сопряжённое к сопряжённому, вообще говоря, с исходным не совпадает. Пространства, для которых E * * = E называются рефлексивными — только для них, строго говоря, можно употреблять термин двойственное пространство.
Комплексно-сопряжённое пространство
Термин сопряжённое пространство может иметь иное значение для линейных пространств над полем комплексных чисел: пространство 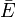 , совпадающее с E как вещественное линейное пространство, но с другой структурой умножения на комплексные числа (см. en:Complex conjugate vector space):
, совпадающее с E как вещественное линейное пространство, но с другой структурой умножения на комплексные числа (см. en:Complex conjugate vector space):
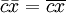
При наличии в пространстве эрмитовой метрики (например, в гильбертовом пространстве) линейно- и комплексно-сопряжённые пространства совпадают.
См. также
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Двойственное пространство" в других словарях:
Комплексно-сопряжённое пространство — Сопряжённое пространство, двойственное пространство в алгебре и функциональном анализе термин, применяющийся при описании двойственности линейных пространств. Как правило, под сопряжённым пространством понимают линейно сопряжённое пространство, т … Википедия
Нормированное векторное пространство — У этого термина существуют и другие значения, см. Пространство. В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина… … Википедия
Сопряжённое пространство — или двойственное пространство пространство линейных функционалов на данном линейном пространстве. Содержание 1 Линейно сопряжённое пространство определение 2 Свойства … Википедия
Нормированное пространство — В трёхмерном пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина нуль вектора, , равна нулю; длина любого другого вектора… … Википедия
Линейное нормированное пространство — В евклидовом пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина нуль вектора, , равна нулю; длина любого другого вектора… … Википедия
КОПСЕВДОГАЛИЛЕЕВО ПРОСТРАНСТВО — пространство, двойственное псевдогалилееву пространству. Оно является частным случаем полугиперболического пространства. Лит.:[1] Р о з е н ф е л ь д Б. А., Неевклидовы пространства, М., 1969. Л. А. Сидоров. КОПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО… … Математическая энциклопедия
Ко-касательное пространство — Кокасательное пространство (иногда неверно ко касательное пространство) пространство, двойственное (сопряженное) касательному. Кокасательное пространство к гладкому многообразию M в точке p обычно обозначается . Сечениями кокасательного… … Википедия
ЗАРИСКОГО КАСАТЕЛЬНОЕ ПРОСТРАНСТВО — к алгебраическому многообразию или схеме Xв точке х векторное пространство над полем вычетов (х)точки х, двойственное к пространству где максимальный идеал локального кольца О X, x точки хна X. Если и задается системой уравнений где то 3. к. п. в … Математическая энциклопедия
КО-Н-ПРОСТРАНСТВО — топологическое пространство, двойственное Н пространству … Математическая энциклопедия
УНИТАРНОЕ ПРЕДСТАВЛЕНИЕ — топологической группы представление топологич. группы унитарными операторами в гильбертовом пространстве. Теория У. п. один из наиболее разработанных разделов теории представлений топологич. групп, что связано как с его многочисленными… … Математическая энциклопедия
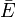 , совпадающее с E как вещественное линейное пространство, но с другой структурой умножения на комплексные числа (см. en:Complex conjugate vector space):
, совпадающее с E как вещественное линейное пространство, но с другой структурой умножения на комплексные числа (см. en:Complex conjugate vector space):