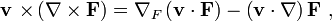- Вихрь (вектор)
-
Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем. Показывает, насколько и в каком направлении закручено поле в каждой точке. Ротор поля F обозначается символом rot F (в русскоязычной литературе) или curl F (в англоязычной литературе), а также
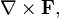 где
где  — векторный дифференциальный оператор набла.
— векторный дифференциальный оператор набла.Содержание
Математическое определение
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:
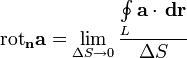 .
.
Нормаль
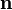 к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.
к площадке направлена так, чтобы при вычислении циркуляции обход по контуру L совершался против часовой стрелки.В трёхмерной декартовой системе координат
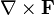 вычисляется следующим образом:
вычисляется следующим образом:Для удобства запоминания можно условно представлять ротор как векторное произведение:
где i, j и k — единичные орты для осей x, y и z соответственно.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).
Физическая интерпретация
По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением
где
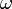 — вектор углового вращения элемента среды в точке О, а
— вектор углового вращения элемента среды в точке О, а  — квадратичная форма от координат — потенциал деформации элемента среды.
— квадратичная форма от координат — потенциал деформации элемента среды.Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор
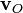 ), вращательного движения (вектор
), вращательного движения (вектор 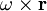 ) и потенциального движения — деформации (вектор
) и потенциального движения — деформации (вектор 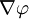 ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство
). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство 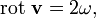 и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.
и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то в северном полушарии для антициклона, вращающегося по часовой стрелке, ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют прямолинейно и с одинаковой скоростью, ротор будет равен нулю (у неоднородного прямолинейного течения ротор ненулевой).
Основные свойства
Следующие свойства могут быть получены из обычных правил дифференцирования.
- Линейность:
для любых векторных полей F и G и для всех вещественных чисел a и b.
- Если
 — скалярное поле, а F — векторное, тогда:
— скалярное поле, а F — векторное, тогда:
или
- Дивергенция ротора равна нулю:
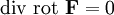 или
или 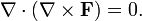
При этом верно и обратное: если поле F бездивергентно, оно есть поле вихря некоторого поля G:
- Если поле F потенциально, его ротор равен нулю (поле F — безвихревое):
Верно и обратное: если поле безвихревое, то оно потенциально:
для некоторого скалярного поля
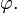
- Теорема Стокса: циркуляция вектора по замкнутому контуру, являющемуся границей некоторой поверхности, равна потоку ротора этого вектора через эту поверхность:
Ротор в ортогональных криволинейных координатах
![+ \frac{1}{H_3H_1}\left[\frac{\partial}{\partial q_3}(A_1H_1) - \frac{\partial}{\partial q_1}(A_3H_3)\right]\mathbf{q_2} + \frac{1}{H_1H_2}\left[\frac{\partial}{\partial q_1}(A_2H_2) - \frac{\partial}{\partial q_2}(A_1H_1)\right]\mathbf{q_3},](/pictures/wiki/files/56/85425d94db549ba72b40f5c0e9152e66.png)
где Hi — коэффициенты Ламе.
Примеры
Простое векторное поле
Рассмотрим векторное поле, линейно зависящее от координат x и y:
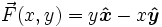 .
.
Очевидно, что поле закручено. Если мы поместим колесо с лопастями в любой области поля, мы увидим, что оно начнет вращаться по направлению часовой стрелки. Используя правило правой руки, можно ожидать ввинчивание поля в страницу. Для правой системы координат направление в страницу будет означать отрицательное направление по оси z.
Вычислим ротор:
Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор является константой, так как он независим от координаты. Количество вращения в приведенном выше векторном поле одно и то же в любой точке (x,y). График ротора F не слишком интересен:
Более сложный пример
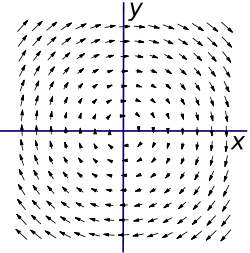
Теперь рассмотрим несколько более сложное векторное поле:
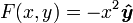 .
.
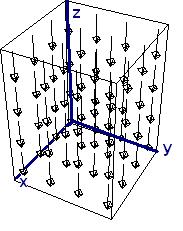
Его график:
Мы можем не увидеть никакого вращения, но, посмотрев повнимательнее направо, мы видим большее поле в, например, точке x=4, чем в точке x=3. Если бы мы установили маленькое колесо с лопастями там, больший поток на правой стороне заставил бы колесо вращаться по часовой стрелке, что соответствует ввинчиванию в направлении -z. Если бы мы расположили колесо в левой части поля, больший поток на его левой стороне заставил бы колесо вращаться против часовой стрелке, что соответствует ввинчиванию в направлении +z. Проверим нашу догадку с помощью вычисления:
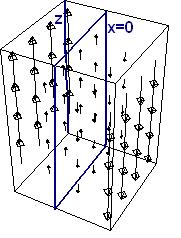
Действительно, ввинчивание происходит в направлении +z для отрицательных x и -z для положительных x, как и ожидалось. Так как этот ротор не одинаков в каждой точке, его график выглядит немного интереснее:
Ротор F с плоскостью x=0, выделенной темно-синим цветомМожно заметить, что график этого ротора не зависит от y или z (как и должно быть) и направлен по -z для положительных x и в направлении +z для отрицательных x.
Три общих примера
Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что
Если v и ∇ поменять местами:
что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.
Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:
что можно считать частным случаем первого примера с подстановкой v → ∇.
Поясняющие примеры
- В смерче ветры вращаются вокруг центра, и векторное поле скоростей ветра имеет ненулевой ротор везде. (см. Вихревое движение).
- В векторном поле, описывающем линейные скорости движения каждой точки вращающегося диска ротор был бы постоянным во всех частях диска.
- Если бы скорости автомобилей на трассе описывались векторным полем, и разные полосы имели разные ограничения по скорости движения, ротор на границе между полосами был бы ненулевым.
- Закон электромагнитной индукции Фарадея, одно из уравнений Максвелла, может быть выражен очень просто через понятие ротора. Он говорит, что ротор электрического поля равен скорости изменения магнитного поля, взятой с обратным знаком, а ротор напряжённости магнитного поля равен сумме плотностей тока обычного и тока смещения.
Примечания
- ↑ Математический словарь высшей школы. В. Т. Воднев, А. Ф. Наумович, Н. Ф. Наумович
См. также
Wikimedia Foundation. 2010.

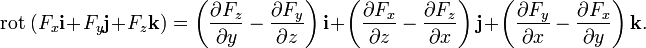
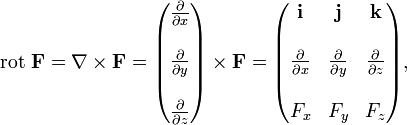
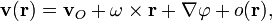
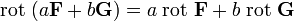
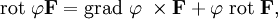
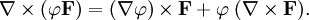
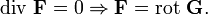
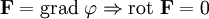
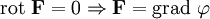
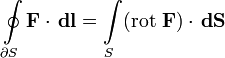
![\operatorname{rot}\;\mathbf{A} = \operatorname{rot}\;(\mathbf{q_1}A_1 + \mathbf{q_2}A_2 + \mathbf{q_3}A_3) = \frac{1}{H_2H_3}\left[\frac{\partial}{\partial q_2}(A_3H_3) - \frac{\partial}{\partial q_3}(A_2H_2)\right]\mathbf{q_1} +](/pictures/wiki/files/102/ffb673a3dba35b73ce0df468756ec0c3.png)
![\vec{\nabla} \times \vec{F} =0\boldsymbol{\hat{x}}+0\boldsymbol{\hat{y}}+ [{\frac{\partial}{\partial x}}(-x) -{\frac{\partial}{\partial y}} y]\boldsymbol{\hat{z}}=-2\boldsymbol{\hat{z}}](/pictures/wiki/files/51/308266a9235d72638006c5b51bd0faea.png)

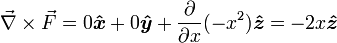
![\mathbf{ \nabla \times} \left( \mathbf{v \times F} \right) = \left[ \left( \mathbf{ \nabla \cdot F } \right) + \mathbf{F \cdot \nabla} \right] \mathbf{v}- \left[ \left( \mathbf{ \nabla \cdot v } \right) + \mathbf{v \cdot \nabla} \right] \mathbf{F} \ .](/pictures/wiki/files/50/2628b53319924465c2409f2d3b024ef5.png)