Больших чисел закон усиленный
- Больших чисел закон усиленный
-
Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.
Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.
Слабый закон больших чисел
Пусть есть бесконечная последовательность одинаково распределённых и некоррелированных случайных величин 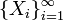 , определённых на одном вероятностном пространстве
, определённых на одном вероятностном пространстве 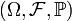 . То есть их ковариация
. То есть их ковариация 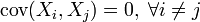 . Пусть
. Пусть 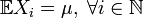 . Обозначим Sn выборочное среднее первых n членов:
. Обозначим Sn выборочное среднее первых n членов:
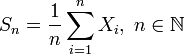 .
.
Тогда 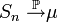 .
.
Усиленный закон больших чисел
Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин 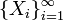 , определённых на одном вероятностном пространстве
, определённых на одном вероятностном пространстве 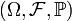 . Пусть
. Пусть 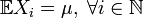 . Обозначим Sn выборочное среднее первых n членов:
. Обозначим Sn выборочное среднее первых n членов:
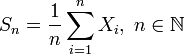 .
.
Тогда 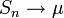 почти наверное.
почти наверное.
См. также
Литература
- Ширяев А. Н. Вероятность, — М.: Наука. 1989.
- Чистяков В. П. Курс теории вероятностей, — М., 1982.
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Больших чисел закон усиленный" в других словарях:
Больших чисел закон — Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В… … Википедия
БОЛЬШИХ ЧИСЕЛ ЗАКОН — общий принцип, в силу к рого совместное действие случайных факторов приводит при нек рых весьма общих условиях к результату, почти не зависящему от случая. Сближение частоты наступления случайного события с его вероятностью при возрастании числа… … Математическая энциклопедия
Усиленный закон больших чисел — Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В… … Википедия
Закон больших чисел — в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости … Википедия
БОЛЬШИХ ЧИСЕЛ УСИЛЕННЫЙ ЗАКОН — одна из форм больших чисел закона (вего общем понимании), утверждающая, что при определенных условиях с вероятностью единица происходит неограниченное сближение средних арифметических последовательности случайных величин с нек рыми постоянными… … Математическая энциклопедия
БОРЕЛЯ УСИЛЕННЫЙ ЗАКОН БОЛЬШИХ ЧИСЕЛ — исторически первый вариант больших чисел усиленного закона, сформулированный И доказанный Э. Борелем [1] применительно к схеме Бернулли (см. Бернулли испытания). Пусть независимые случайные величины одинаково распределены и принимают два значения … Математическая энциклопедия
ЗБЧ — Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В… … Википедия
УЗБЧ — Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В… … Википедия
ВЕРОЯТНОСТЕЙ ТЕОРИЯ — математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных к. л. образом с первыми. Утверждение о том, что к. л. событие наступает с вероятностью, равной, напр., 1/2, еще не… … Математическая энциклопедия
БЕРНУЛЛИ ИСПЫТАНИЯ — независимые испытания с двумя исходами каждое ( успехом и неудачей ) и такие, что вероятности исходов не изменяются от испытания к испытанию. Б. и. служат одной из основных схем, рассматриваемых в теории вероятностей. Пусть р вероятность успеха и … Математическая энциклопедия
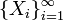 , определённых на одном вероятностном пространстве
, определённых на одном вероятностном пространстве 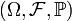 . То есть их ковариация
. То есть их ковариация 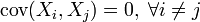 . Пусть
. Пусть 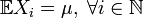 . Обозначим Sn выборочное среднее первых n членов:
. Обозначим Sn выборочное среднее первых n членов: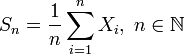 .
.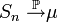 .
.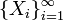 , определённых на одном вероятностном пространстве
, определённых на одном вероятностном пространстве 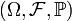 . Пусть
. Пусть 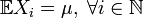 . Обозначим Sn выборочное среднее первых n членов:
. Обозначим Sn выборочное среднее первых n членов: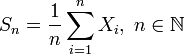 .
.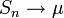 почти наверное.
почти наверное.