- ЗБЧ
-
Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.
Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.
Содержание
Слабый закон больших чисел
Пусть есть бесконечная последовательность одинаково распределённых и некоррелированных случайных величин
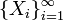 , определённых на одном вероятностном пространстве
, определённых на одном вероятностном пространстве 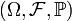 . То есть их ковариация
. То есть их ковариация 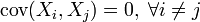 . Пусть
. Пусть 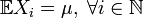 . Обозначим Sn выборочное среднее первых n членов:
. Обозначим Sn выборочное среднее первых n членов: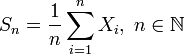 .
.
Тогда
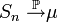 .
.Усиленный закон больших чисел
Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин
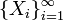 , определённых на одном вероятностном пространстве
, определённых на одном вероятностном пространстве 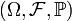 . Пусть
. Пусть 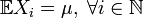 . Обозначим Sn выборочное среднее первых n членов:
. Обозначим Sn выборочное среднее первых n членов: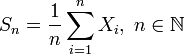 .
.
Тогда
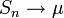 почти наверное.
почти наверное.См. также
Литература
- Ширяев А. Н. Вероятность, — М.: Наука. 1989.
- Чистяков В. П. Курс теории вероятностей, — М., 1982.
Wikimedia Foundation. 2010.
