Бесконечно малая

Бесконечно малая величина — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая величина — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Исчисление бесконечно малых и больших

Исчисление бесконечно малых — вычисления, производимые с бесконечно малыми величинами, при которых производный результат рассматривается как бесконечная сумма бесконечно малых. Исчисление бесконечно малых величин является общим понятием для дифференциальных и интегральных исчислений, составляющих основу современной высшей математики. Понятие бесконечно малой величины тесно связано с понятием предела.

Бесконечно малая

Последовательность a_n называется бесконечно малой, если 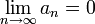$\lim_{n\to\infty}a_n=0$. Например, последовательность чисел 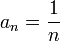$a_n=\frac{1}{n}$ — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если $\lim_{x\to x_0}f(x)=0$.

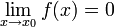Функция называется бесконечно малой на бесконечности, если 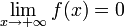$\lim_{x\to+\infty}f(x)=0$ либо $\lim_{x\to-\infty}f(x)=0$.

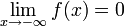Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если 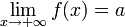$\lim_{x\to+\infty}f(x)=a$, то f(x) − a = α(x), $\lim_{x\to+\infty}(f(x)-a)=0$.

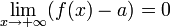Бесконечно большая величина

Последовательность a_n называется бесконечно большой, если $\lim_{n\to\infty}a_n=\infty$.

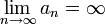Функция называется бесконечно большой в окрестности точки x₀, если $\lim_{x\to x_0}f(x)=\infty$.

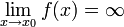Функция называется бесконечно большой на бесконечности, если 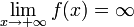$\lim_{x\to+\infty}f(x)=\infty$ либо $\lim_{x\to-\infty}f(x)=\infty$.

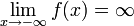Во всех случаях бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsinx не является бесконечно большой при $x\to+\infty$.

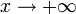Свойства бесконечно малых и бесконечно больших

• Сумма конечного числа бесконечно малых — бесконечно малая.
• Произведение бесконечно малых — бесконечно малая.
• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
• Если a_n — бесконечно малая последовательность, сохраняющая знак, то 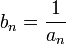$b_n=\frac{1}{a_n}$ — бесконечно большая последовательность.

Сравнение бесконечно малых величин

Как сравнивать бесконечно малые величины?
Отношение бесконечно малых величин образует так называемую неопределённость $\frac{0}{0}$.

Определения

Допустим, у нас есть бесконечно малые при одном и том же 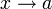$x\to a$ величины α(x) и β(x) (либо, что не суть важно для определения, бесконечно малые последовательности).

• Если 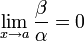$\lim_{x\to a}\frac{\beta}{\alpha}=0$, то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).
• Если 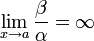$\lim_{x\to a}\frac{\beta}{\alpha}=\infty$, то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

• Если 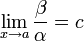$\lim_{x\to a}\frac{\beta}{\alpha}=c$ (предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости.
  Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

• Если 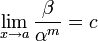$\lim_{x\to a}\frac{\beta}{\alpha^m}=c$ (предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Для вычисления подобных пределов удобно использовать правило Лопиталя.

Примеры сравнения

• При 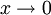${x\to 0}$ величина x⁵ имеет высший порядок малости относительно x³, так как 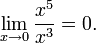$\lim_{x\to 0}\frac{x^5}{x^3} = 0.$ С другой стороны, x³ имеет низший порядок малости относительно x⁵, так как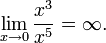 $\lim_{x\to 0}\frac{x^3}{x^5} = \infty.$
  

С использованием О-символики полученные результаты могут быть записаны в следующем виде x⁵ = o(x³).

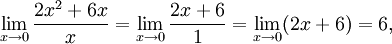• $\lim_{x\to 0}\frac{2x^2+6x}{x}=\lim_{x\to 0}\frac{2x+6}{1}=\lim_{x\to 0}(2x+6)=6,$ то есть при 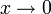$x\to 0$ функции f(x) = 2x² + 6x и g(x) = x являются бесконечно малыми величинами одного порядка.
  

В данном случае справедливы записи 2x² + 6x = O(x) и x = O(2x² + 6x).

• При 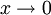${x\to 0}$ бесконечно малая величина 2x³ имеет третий порядок малости относительно x, поскольку 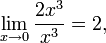$\lim_{x\to 0}\frac{2x^3}{x^3} = 2,$ бесконечно малая 0,7x² — второй порядок, бесконечно малая 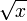$\sqrt {x}$ — порядок 0,5.

Эквивалентные величины

Определение

Если 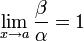$\lim_{x\to a}\frac{\beta}{\alpha}=1$, то бесконечно малые величины α и β называются эквивалентными ($\alpha\thicksim\beta$).
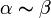Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При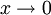 ${x\to 0}$ справедливы следующие соотношения эквивалентности:   $\sin x \thicksim x$,       $\mathrm{tg} x\thicksim x$,       $\ln(1+x) \thicksim x$.

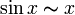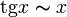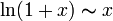Теорема

Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.

Данная теорема имеет прикладное значение при нахождении пределов (см. пример).

Пример использования

• Найти $\lim_{x\to 0}\frac{\sin 2x}{x}.$
  

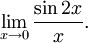
Заменяя sin2x эквивалентной величиной 2x, получаем   $\lim_{x\to 0}\frac{\sin 2x}{x} = \lim_{x\to 0}\frac{2x}{x} = 2.$

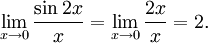
Исторический очерк

Понятие «бесконечно малое» обсуждалось ещё в античные времена в связи с концепцией неделимых атомов, однако в классическую математику не вошло. Вновь оно возродилось с появлением в XVI веке «метода неделимых» — разбиения исследуемой фигуры на бесконечно малые сечения.

В XVII веке произошла алгебраизация исчисления бесконечно малых. Они стали определяться как числовые величины, которые меньше всякой конечной (ненулевой) величины и всё же не равны нулю. Искусство анализа заключалось в составлении соотношения, содержащего бесконечно малые (дифференциалы), и затем — в его интегрировании.

Математики старой школы подвергли концепцию бесконечно малых резкой критике. Мишель Ролль писал, что новое исчисление есть «набор гениальных ошибок»; Вольтер ядовито заметил, что это исчисление представляет собой искусство вычислять и точно измерять вещи, существование которых не может быть доказано. Даже Гюйгенс признавался, что не понимает смысла дифференциалов высших порядков.

Споры в Парижской Академии наук по вопросам обоснования анализа приобрели настолько скандальный характер, что Академия однажды вообще запретила своим членам высказываться на эту тему (в основном это касалось Ролля и Вариньона). В 1706 году Ролль публично снял свои возражения, однако дискуссии продолжались.

В 1734 году известный английский философ, епископ Джордж Беркли выпустил нашумевший памфлет, известный под сокращенным названием «Аналист». Полное его название: «Аналист или рассуждение, обращенное к неверующему математику, где исследуется, более ли ясно воспринимаются или более ли очевидно выводятся предмет, принципы и умозаключения современного анализа, чем религиозные таинства и догматы веры».

«Аналист» содержал остроумную и во многом справедливую критику исчисления бесконечно малых. Метод анализа Беркли считал несогласным с логикой и писал, что, «как бы он ни был полезен, его можно рассматривать только как некую догадку; ловкую сноровку, искусство или скорее ухищрение, но не как метод научного доказательства». Цитируя фразу Ньютона о приращении текущих величин «в самом начале их зарождения или исчезновения», Беркли иронизирует: «это ни конечные величины, ни бесконечно малые, ни даже ничто. Не могли ли бы мы их назвать призраками почивших величин?… И как вообще можно говорить об отношении между вещами, не имеющими величины?.. Тот, кто может переварить вторую или третью флюксию [производную], вторую или третью разность, не должен, как мне кажется, придираться к чему-либо в богословии».

Невозможно, пишет Беркли, представить себе мгновенную скорость, то есть скорость в данное мгновение и в данной точке, ибо понятие движения включает понятия о (конечных ненулевых) пространстве и времени.

Как же с помощью анализа получаются правильные результаты? Беркли пришел к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Занятно, что некоторые крупные математики (например, Лагранж) согласились с ним.

Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция. И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.

В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс.

Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа.

См. также

• «O» большое и «o» малое
• Дифференциал
• Метод неделимых
• Предел последовательности
• Предел функции