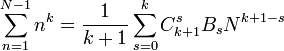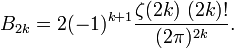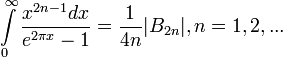Бернулли числа — специальная последовательность рациональных чисел, фигурирующая в различных вопросах математического анализа и теории чисел. Значения первых шести Б. ч.: B1 = 1/6, B2 = 1/30, B3 = 1/42, B4 = 1/30, B5 = 5/66, B6 =… … Большая советская энциклопедия
БЕРНУЛЛИ ЧИСЛА — последовательность рациональных чисел найденная Я. Бернулли [1] в связи с вычислением суммы одинаковых стейеней натуральных чисел: Значения первых Б. ч.: Все Б. ч. с нечетными номерами, кроме В 1 равны нулю, знаки чередуются. Б. ч. являются… … Математическая энциклопедия
Бернулли, Якоб — Якоб Бернулли Jakob Bernoulli … Википедия
Бернулли, Яков — Якоб Бернулли Jakob Bernoulli Якоб Бернулли (Якоб I) Дата рождения: 27 декабря 1654 Место рождения: Базель Дата смерти: 16 августа 1705 Место смерти … Википедия
Бернулли Якоб — Якоб Бернулли Jakob Bernoulli Якоб Бернулли (Якоб I) Дата рождения: 27 декабря 1654 Место рождения: Базель Дата смерти: 16 августа 1705 Место смерти … Википедия
Бернулли Я. — Якоб Бернулли Jakob Bernoulli Якоб Бернулли (Якоб I) Дата рождения: 27 декабря 1654 Место рождения: Базель Дата смерти: 16 августа 1705 Место смерти … Википедия
БЕРНУЛЛИ МНОГОЧЛЕНЫ — многочлены вида где Bs Бернулли числа. Так, для n=0, 1, 2, 3 Б. м. можно вычислять по рекуррентной формуле Для натурального Б. м. впервые рассматривались Я. Бернулли (J. Bernoulli, 1713) в связи с вычислением суммы При произвольном хБ. м. впервые … Математическая энциклопедия
Бернулли — (Bernoulli) семья швейцарских учёных, родоначальник которой Якоб Б. (умер 1583) был выходцем из Голландии. Якоб Б. (27.12.1654, Базель, 16.8.1705, там же), профессор математики Базельского университета (1687). Ознакомившись в… … Большая советская энциклопедия
БЕРНУЛЛИ Якоб — БЕРНУЛЛИ (Bernoulli) Якоб (1654 1705), брат Иоганна Бернулли (см. БЕРНУЛЛИ Иоганн); профессор математики Базельского университета (с 1687). Ознакомившись в 1686 с первым мемуаром Г. Лейбница (см. ЛЕЙБНИЦ Готфрид Вильгельм) по дифференциальному… … Энциклопедический словарь
Бернулли — (Bernoulli) семейство, давшее ряд замечательных людей,преимущественно в области математических наук. Родоначальник его Яков Б.(ум. 1583 г.), эмигрировал из Антверпена вовремя управления Фландриейгерцога Альбы во Франкфурт; внук его, также Яков Б … Энциклопедия Брокгауза и Ефрона
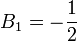
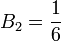
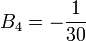
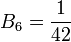
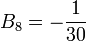
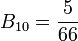
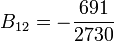
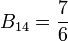
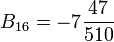
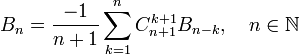
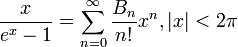 ,
,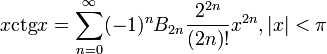 ,
,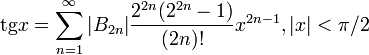 .
.