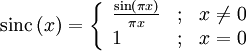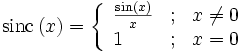- Sinc-функция
-
 Графики нормированной и ненормированной функций sinc (x) в диапазоне −10π ≤ x ≤ 10π
Графики нормированной и ненормированной функций sinc (x) в диапазоне −10π ≤ x ≤ 10πSinc-функция, обозначаемая
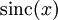 , (от лат. sinus cardinalis — кардинальный синус) имеет два определения, соответственно для нормированной sinc-функции и ненормированной sinc-функции:
, (от лат. sinus cardinalis — кардинальный синус) имеет два определения, соответственно для нормированной sinc-функции и ненормированной sinc-функции:- В цифровой обработке сигналов и теории связи нормированная sinc-функция обычно определяется как
- В математике ненормированная sinc-функция определяется как
В обоих случаях значение функции в особой точке x = 0 явным образом задаётся равным единице (см. замечательные пределы). Таким образом, sinc-функция аналитична для любого значения аргумента.
Свойства
Нормированная sinc-функция обладает следующими свойствами:
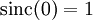 и
и 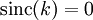 для
для 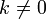 и
и 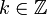 (целые числа); то есть, это интерполирующая функция
(целые числа); то есть, это интерполирующая функция- функции
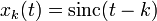 формируют ортонормированный базис для функций в функциональном пространстве
формируют ортонормированный базис для функций в функциональном пространстве 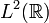 , с наибольшей круговой частотой
, с наибольшей круговой частотой 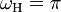 .
.
- Локальные максимум и минимум ненормированной sinc-функции,
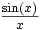 совпадают со значениями косинуса, то есть там, где производная
совпадают со значениями косинуса, то есть там, где производная 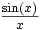 равна нулю (локальный экстремум в точке
равна нулю (локальный экстремум в точке 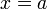 ), выполняется условие
), выполняется условие 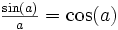 .
.
- Ненормированная sinc-функция является сферической функцией Бесселя первого рода нулевого порядка,
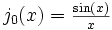 . Нормированная sinc-функция —
. Нормированная sinc-функция — 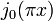 .
.
- Ненормированная sinc-функция обращается в ноль при значениях аргумента, кратных
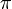 ; нормированная sinc-функция —
; нормированная sinc-функция — 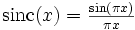 при целых значениях аргумента.
при целых значениях аргумента.
- Непрерывное преобразование Фурье нормированной sinc-функции
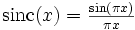 (для единичного интервала частот) равно прямоугольной функции
(для единичного интервала частот) равно прямоугольной функции 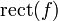 .
.
-
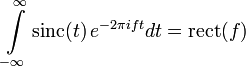 ,
,
- где прямоугольная функция — функция, принимающая значения, равные 1 для любого аргумента из интервала между −1/2 и 1/2, и равная нулю при любом другом значении аргумента.
- Разложение по степеням х:
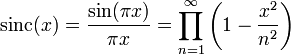
- Выражение через гамма-функцию:
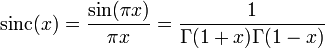
- где Γ(x) — гамма-функция.
См. также
- В цифровой обработке сигналов и теории связи нормированная sinc-функция обычно определяется как
Wikimedia Foundation. 2010.