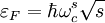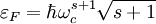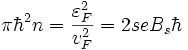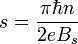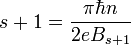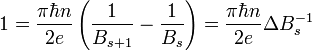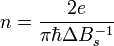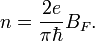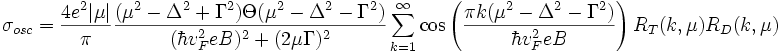Осцилляции Шубникова — де Гааза (графен)

Осцилляции Шубникова — де Гааза (графен)

Графен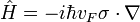

$\hat{H}=-i\hbar v_F\sigma\cdot\nabla$

Уравнение Дирака (графен)

Введение ... Математическая формулировка ... Основа Квантовая механика · Уравнение Дирака Нейтрино · (2+1)-мерная КЭД · Постоянная тонкой структуры · Фаза Берри · Углеродные нанотрубки Фундаментальные понятия Зонная структура · Уравнение Дирака · Киральность · Гексагональная решётка · Волновая функция · Точка электронейтральности · Видимость графена · Фаза Берри Получение и технология Получение графена · Механическое отшелушивание · Химическое расщепление графита · Рост графеновых плёнок · Подвешенный графен · Верхний затвор Применения Графеновый полевой транзистор Графеновые наноленты Транспортные свойства Электроны и дырки · Проводимость · Фононы· Парадокс Клейна · Линза Веселаго · 1/f · Дробовой шум Случайный телеграфный сигнал · p — n переход · Ферми жидкость Магнитное поле Магнетосопротивление · Осцилляции Шубникова — деГааза · КЭХ · Спиновый квантовый эффект Холла · ДКЭХ · Осцилляции Вейса · Магнетоэкситоны · Сверхпроводимость · Слабая локализация · Эффект Ааронова — Бома Оптика графена Рамановское рассеяние света Известные учёные Андре Гейм

Осцилляции Шубникова — де Гааза в графене впервые наблюдали в 2005 году.^[1][2] Эффект заключается в периодическом изменении сопротивления или проводимости электронного или дырочного газа как функции обратного магнитного поля. Он связан с осциллирующим поведением плотности состояний^[3] в магнитном поле.

Период осцилляций

Энергия дираковских безмассовых фермионов в магнитном поле пропорциональна корню из магнитного поля и при заполнении s и s+1 релятивистских уровней Ландау можно записать для электронов на уровне Ферми (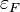$\varepsilon_F$) следующие соотношения

$\varepsilon_F=\hbar\omega_{c}^s\sqrt{s}$

$\varepsilon_F=\hbar\omega_{c}^{s+1}\sqrt{s+1}$

где «циклотронная частота» 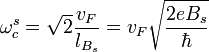$\omega_{c}^s=\sqrt{2}\frac{v_F}{l_{B_s}}=v_F\sqrt{\frac{2eB_s}{\hbar}}$, а магнитная длина 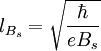$l_{B_s}=\sqrt{\frac{\hbar}{eB_s}}$, s — натуральное число 1, 2, 3, …, v_F — фермиевская скорость, 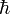$\hbar$ — постоянная Планка, e — элементарный заряд, B_s — магнитное поле соответствующее s-ому уровню Ландау. Концентрация электронов без магнитного поля равна 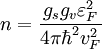$n=\frac{g_sg_v\varepsilon_F^2}{4\pi\hbar^2v_F^2}$. Используя это соотношение при условии, что магнитное поле не изменяет уровень Ферми (например он зафиксирован по внешним причинам) получим

$\pi\hbar^2n=\frac{\varepsilon_F^2}{v_F^2}=2seB_s\hbar$

или

$s=\frac{\pi\hbar n}{2eB_s}$

$s+1=\frac{\pi\hbar n}{2eB_{s+1}}$

Вычитая из последнего равенства предпоследнее найдём соотношение для периода осцилляций $\Delta B_s^{-1}$

$1=\frac{\pi\hbar n}{2e}\left(\frac{1}{B_{s+1}}-\frac{1}{B_s}\right)=\frac{\pi\hbar n}{2e}\Delta B_s^{-1}$

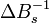
Здесь можно определить концентрацию носителей через период

$n=\frac{2e}{\pi\hbar\Delta B_s^{-1}}$

или фундаментальную частоту B_F

$n=\frac{2e}{\pi\hbar}B_F.$

Эта формула аналогична формуле для концентрации двумерного электронного газа в инверсионных слоях кремния (100).

Теория Гусынина — Шарапова

В статье^[4] Гусынина и Шарапова показано, что осциллирующую часть продольной компоненты тензора проводимости можно записать в виде

$\sigma_{osc}=\frac{4e^2|\mu|}{\pi}\frac{(\mu^2-\Delta^2+\Gamma^2)\Theta(\mu^2-\Delta^2-\Gamma^2)}{(\hbar v_F^2eB)^2+(2\mu\Gamma)^2}\sum_{k=1}^{\infty}\cos\left(\frac{\pi k(\mu^2-\Delta^2-\Gamma^2)}{\hbar v_F^2eB}\right)R_T(k,\mu)R_D(k,\mu)$

где μ — химический потенциал, Δ — ширина запрещённой зоны (в случае графена равна нулю), Γ — ширина уровня Ландау (не зависит от магнитного поля и температуры), Θ(x) — ступенчатая функция, амплитудный температурный множитель равен

$R_T(k,\mu)=\frac{2\pi^2kT\mu/\hbar v_F^2eB}{\sinh(2\pi^2kT\mu/\hbar v_F^2eB)}$,

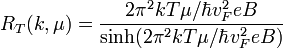а множитель Дингля

$R_D(k,\mu)=\exp\left(\frac{-2\pi k|\mu|\Gamma}{\hbar v_F^2eB}\right).$.

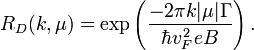Формула описывает осцилляции Шубникова — де Гааза не очень близко к точке электронейтральности. В окрестностях самой точки осцилляции магнетопроводимости отсутствуют. При больших концентрациях носителей можно пренебречь шириной запрещённой зоны и уширением уровней Ландау (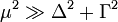$\mu^2\gg \Delta^2+\Gamma^2$) и частота осцилляций по обратному магнитному полю совпадает с формулой полученной ранее.

Примечания

1. ↑ Novoselov K. S. et al. «Two-dimensional gas of massless Dirac fermions in graphene», Nature 438, 197 (2005) DOI:10.1038/nature04233
2. ↑ Zhang Y.et. al. «Experimental observation of the quantum Hall effect and Berry’s phase in graphene» Nature 438, 201 (2005) DOI:10.1038/nature04235
3. ↑ Sharapov S. G. et. al. Magnetic oscillations in planar systems with the Dirac-like spectrum of quasiparticle excitations Phys. Rev. B 69, 075104 (2004) DOI:10.1103/PhysRevB.69.075104
4. ↑ Gusynin V. P. and Sharapov S. G. Magnetic oscillations in planar systems with the Dirac-like spectrum of quasiparticle excitations. II. Transport properties Phys. Rev. B 71, 125124 (2005) DOI:10.1103/PhysRevB.71.125124